In quantum mechanics, bra–ket notation is a standard notation for describing quantum states. It can also be used to denote abstract vectors and linear functionals in mathematics. The notation uses angle brackets and a vertical bar, to denote the scalar product of vectors or the action of a linear functional on a vector in a complex vector space. The scalar product or action is written as
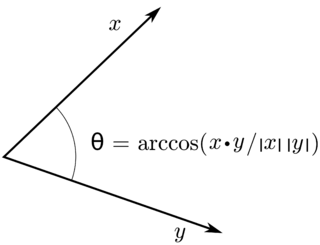
In linear algebra, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors. Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the angle between two vectors. They also provide the means of defining orthogonality between vectors. Inner product spaces generalize Euclidean spaces to vector spaces of any dimension, and are studied in functional analysis. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.

In geometry and physics, spinors are elements of a (complex) vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. However, when a sequence of such small rotations is composed (integrated) to form an overall final rotation, the resulting spinor transformation depends on which sequence of small rotations was used: unlike vectors and tensors, a spinor transforms to its negative when the space is rotated through a complete turn from 0° to 360°. This property characterizes spinors. It is also possible to associate a substantially similar notion of spinor to Minkowski space in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in geometry by Élie Cartan in 1913. In the 1920s physicists discovered that spinors are essential to describe the intrinsic angular momentum, or "spin", of the electron and other subatomic particles.

A vector space is a collection of objects called vectors, which may be added together and multiplied ("scaled") by numbers, called scalars. Scalars are often taken to be real numbers, but there are also vector spaces with scalar multiplication by complex numbers, rational numbers, or generally any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called axioms, listed below.

In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. A feature of quaternions is that multiplication of two quaternions is noncommutative. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space or equivalently as the quotient of two vectors.

In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. For example, the complex conjugate of 3 + 4i is 3 − 4i.
In mathematics, the Cayley–Dickson construction, named after Arthur Cayley and Leonard Eugene Dickson, produces a sequence of algebras over the field of real numbers, each with twice the dimension of the previous one. The algebras produced by this process are known as Cayley–Dickson algebras, for example complex numbers, quaternions, and octonions. These examples are useful composition algebras frequently applied in mathematical physics.
In mathematics, more specifically in functional analysis, a positive linear functional on an ordered vector space is a linear functional f on V so that for all positive elements v of V, that is v≥0, it holds that
In mathematics, more specifically in group theory, the character of a group representation is a function on the group that associates to each group element the trace of the corresponding matrix. The character carries the essential information about the representation in a more condensed form. Georg Frobenius initially developed representation theory of finite groups entirely based on the characters, and without any explicit matrix realization of representations themselves. This is possible because a complex representation of a finite group is determined by its character. The situation with representations over a field of positive characteristic, so-called "modular representations", is more delicate, but Richard Brauer developed a powerful theory of characters in this case as well. Many deep theorems on the structure of finite groups use characters of modular representations.
In mathematical field of representation theory, a quaternionic representation is a representation on a complex vector space V with an invariant quaternionic structure, i.e., an antilinear equivariant map
In the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant map
In mathematics, and especially the discipline of representation theory, the Schur indicator, named after Issai Schur, or Frobenius–Schur indicator describes what invariant bilinear forms a given irreducible representation of a compact group on a complex vector space has. It can be used to classify the irreducible representations of compact groups on real vector spaces.
In mathematics, the Lie–Kolchin theorem is a theorem in the representation theory of linear algebraic groups; Lie's theorem is the analog for linear Lie algebras.

In mathematics, a Cartan subalgebra, often abbreviated as CSA, is a nilpotent subalgebra of a Lie algebra that is self-normalising. They were introduced by Élie Cartan in his doctoral thesis.
In mathematics, if G is a group and ρ is a linear representation of it on the vector space V, then the dual representationρ* is defined over the dual vector space V* as follows:
In mathematics, the complex conjugate of a complex vector space is a complex vector space , which has the same elements and additive group structure as , but whose scalar multiplication involves conjugation of the scalars. In other words, the scalar multiplication of satisfies
In mathematics, if G is a group and Π is a representation of it over the complex vector space V, then the complex conjugate representationΠ is defined over the complex conjugate vector space V as follows:
In mathematics, a unipotent elementr of a ring R is one such that r − 1 is a nilpotent element; in other words, (r − 1)n is zero for some n.
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studies modules over these abstract algebraic structures. In essence, a representation makes an abstract algebraic object more concrete by describing its elements by matrices and the algebraic operations in terms of matrix addition and matrix multiplication. The algebraic objects amenable to such a description include groups, associative algebras and Lie algebras. The most prominent of these is the representation theory of groups, in which elements of a group are represented by invertible matrices in such a way that the group operation is matrix multiplication.
In mathematics and physics, super Minkowski space or Minkowski superspace is a supersymmetric extension of Minkowski space, sometimes used as the base manifold for superfields. It is acted on by the super Poincaré algebra.

William Edgar Fulton is an American mathematician, specializing in algebraic geometry.

Joseph Daniel Harris, known nearly universally as Joe Harris, is a mathematician at Harvard University working in the field of algebraic geometry. He attended college at and received his Ph.D. from Harvard in 1978 under Phillip Griffiths.
Graduate Texts in Mathematics (GTM) is a series of graduate-level textbooks in mathematics published by Springer-Verlag. The books in this series, like the other Springer-Verlag mathematics series, are yellow books of a standard size. The GTM series is easily identified by a white band at the top of the book.








