 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages) (Learn how and when to remove this template message)
|
The mean sojourn time (or sometimes mean waiting time) for an object in a system is the amount of time an object is expected to spend in a system before leaving the system for good.
Imagine you are standing in line to buy a ticket at the counter. If you, after one minute, observe the number of customers that are behind you it might be looked upon as a (rough) estimate of the number of customers entering the system (here, waiting line) per unit time (here, minute). If you then divide the number of customers in front of you with this ”flow” of customers you just estimated the waiting time you should expect; i.e. the time it will take you to reach the counter, and indeed it is a rough estimate.
To formalize this somewhat let us consider the waiting line as a system S into which there is a flow of particles (customers) and where the process “buy ticket” means that the particle leaves the system. The waiting time we have considered above is commonly referred to as transit time, and the theorem we have applied is occasionally called the Little's theorem, which could be formulated as: the expected steady state number of particles in the system S equals the flow of particles into S times the mean transit time. Similar theorems have been discovered in other fields, and in physiology it was earlier known as one of the Stewart-Hamilton equations (e.g. used for estimation of blood volume of organs).
In systems theory, a system or a process is in a steady state if the variables which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties p of the system, the partial derivative with respect to time is zero and remains so:
This principle (or, theorem) can be generalized. Thus, let us consider a system S in the form of a closed domain of finite volume in the Euclidean space. And let us further consider the situation where there is a stream of ”equivalent” particles into S (number of particles per time unit) where each particle retains its identity while being in S and eventually - after a finite time - leaves the system irreversibly (i.e. for these particles the system is ”open”). The Figure
In geometry, Euclidean space encompasses the two-dimensional Euclidean plane, the three-dimensional space of Euclidean geometry, and similar spaces of higher dimension. It is named after the Ancient Greek mathematician Euclid of Alexandria. The term "Euclidean" distinguishes these spaces from other types of spaces considered in modern geometry. Euclidean spaces also generalize to higher dimensions.
depicts the thought motion history of a single such particle, which thus moves in and out of the subsystem s three times, each of which results in a transit time, namely the time spent in the subsystem between entrance and exit. The sum of these transit times is the sojourn time of s for that particular particle. If the motions of the particles are looked upon as realizations of one and the same stochastic process it is meaningful to speak of the mean value of this sojourn time. That is, the mean sojourn time of a subsystem is the total time a particle is expected to spend in the subsystem s before leaving the system S for good.
In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a collection of random variables. Historically, the random variables were associated with or indexed by a set of numbers, usually viewed as points in time, giving the interpretation of a stochastic process representing numerical values of some system randomly changing over time, such as the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. They have applications in many disciplines including sciences such as biology, chemistry, ecology, neuroscience, and physics as well as technology and engineering fields such as image processing, signal processing, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance.
To see a practical significance of this quantity let us accept as a law of physics that, if the stream of particles into S is constant and all other relevant factors are kept constant, S will eventually reach steady state (i.e. the number and distribution of particles is constant everywhere in S). It can then be demonstrated that the steady state number of particles in the subsystem s equals the stream of particles into the system S times the mean sojourn time of the subsystem. This is thus a more general form of what above was referred to as Little's theorem, and it might be called the mass-time equivalence:
which sometimes has been called the occupancy principle (what here is called mean sojourn time is then referred to as occupancy; a perhaps not all that fortunate term, because it suggests the presence of a definite number of “sites” in the system S). This mass-time equivalence has found applications in, say, medicine for the study of metabolism of individual organs.
Metabolism is the set of life-sustaining chemical reactions in organisms. The three main purposes of metabolism are: the conversion of food to energy to run cellular processes; the conversion of food/fuel to building blocks for proteins, lipids, nucleic acids, and some carbohydrates; and the elimination of nitrogenous wastes. These enzyme-catalyzed reactions allow organisms to grow and reproduce, maintain their structures, and respond to their environments..
Again, we deal here with a generalization of what in queuing theory is sometimes referred to as Little's theorem that, and this is important, applies only to the whole system S (not to an arbitrary subsystem as in the mass-time equivalence); the mean sojourn time can in the Little's theorem be interpreted as mean transit time.
As should be evident from the discussion of the figure above, there is a fundamental difference between the meaning of the two quantities sojourn time and transit time: the generality of the mass-time equivalence is very much due to the special meaning of the notion of sojourn time. When the whole system is considered (as in Littl's theorem) is it true that sojourn time always equals transit time.
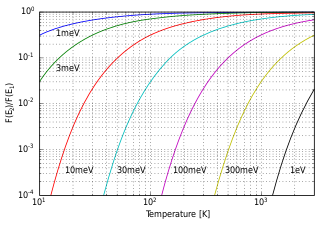
In statistical mechanics and mathematics, a Boltzmann distribution is a probability distribution or probability measure that gives the probability that a system will be in a certain state as a function of that state's energy and the temperature of the system. It is also a frequency distribution of particles in a system. The distribution is expressed in the form
Brownian motion or pedesis is the random motion of particles suspended in a fluid resulting from their collision with the fast-moving molecules in the fluid.
Mass is both a property of a physical body and a measure of its resistance to acceleration when a net force is applied. An object's mass also determines the strength of its gravitational attraction to other bodies.
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, it is a characteristic of the system's total energy and momentum that is the same in all frames of reference related by Lorentz transformations. If a center-of-momentum frame exists for the system, then the invariant mass of a system is equal to its total mass in that "rest frame". In other reference frames, where the system's momentum is nonzero, the total mass of the system is greater than the invariant mass, but the invariant mass remains unchanged.
In queueing theory, a discipline within the mathematical theory of probability, Little's result, theorem, lemma, law, or formula is a theorem by John Little which states that the long-term average number L of customers in a stationary system is equal to the long-term average effective arrival rate λ multiplied by the average time W that a customer spends in the system. Expressed algebraically the law is
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics.
In physics, mass–energy equivalence states that anything having mass has an equivalent amount of energy and vice versa, with these fundamental quantities directly relating to one another by Albert Einstein's famous formula:
Greek letters are used in mathematics, science, engineering, and other areas where mathematical notation is used as symbols for constants, special functions, and also conventionally for variables representing certain quantities. In these contexts, the capital letters and the small letters represent distinct and unrelated entities. Those Greek letters which have the same form as Latin letters are rarely used: capital A, B, E, Z, H, I, K, M, N, O, P, T, Y, X. Small ι, ο and υ are also rarely used, since they closely resemble the Latin letters i, o and u. Sometimes font variants of Greek letters are used as distinct symbols in mathematics, in particular for ε/ϵ and π/ϖ. The archaic letter digamma (Ϝ/ϝ/ϛ) is sometimes used.
A matrix scheme is a business model involving the exchange of money for a certain product with a side bonus of being added to a waiting list for a product of greater value than the amount given. Matrix schemes are also sometimes considered similar to Ponzi or pyramid schemes. They have been called "unsustainable" by the United Kingdom's Office of Fair Trading. A matrix scheme is also an example of an 'exploding queue' in queueing theory.
In queueing theory, a discipline within the mathematical theory of probability, Buzen's algorithm is an algorithm for calculating the normalization constant G(N) in the Gordon–Newell theorem. This method was first proposed by Jeffrey P. Buzen in 1973. Computing G(N) is required to compute the stationary probability distribution of a closed queueing network.
In queueing theory, a discipline within the mathematical theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation. The model is the most elementary of queueing models and an attractive object of study as closed-form expressions can be obtained for many metrics of interest in this model. An extension of this model with more than one server is the M/M/c queue.
In queueing theory, a discipline within the mathematical theory of probability, Burke's theorem is a theorem asserting that, for the M/M/1 queue, M/M/c queue or M/M/∞ queue in the steady state with arrivals a Poisson process with rate parameter λ:
The Ehrenfest model of diffusion was proposed by Tatiana and Paul Ehrenfest to explain the second law of thermodynamics. The model considers N particles in two containers. Particles independently change container at a rate λ. If X(t) = i is defined to be the number of particles in one container at time t, then it is a birth-death process with transition rates
In queueing theory, a discipline within the mathematical theory of probability, the arrival theorem states that "upon arrival at a station, a job observes the system as if in steady state at an arbitrary instant for the system without that job."
In queueing theory, a discipline within the mathematical theory of probability, mean value analysis (MVA) is a recursive technique for computing expected queue lengths, waiting time at queueing nodes and throughput in equilibrium for a closed separable system of queues. The first approximate techniques were published independently by Schweitzer and Bard, followed later by an exact version by Lavenberg and Reiser published in 1980.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian, service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/k queue is a queue model where arrivals are Markovian, service times have a General distribution and there are k servers. The model name is written in Kendall's notation, and is an extension of the M/M/c queue, where service times must be exponentially distributed and of the M/G/1 queue with a single server. Most performance metrics for this queueing system are not known and remain an open problem.
In queueing theory, a discipline within the mathematical theory of probability, a heavy traffic approximation is the matching of a queueing model with a diffusion process under some limiting conditions on the model's parameters. The first such result was published by John Kingman who showed that when the utilisation parameter of an M/M/1 queue is near 1 a scaled version of the queue length process can be accurately approximated by a reflected Brownian motion.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue.
