In mathematics, an associative algebra is an algebraic structure with compatible operations of addition, multiplication, and a scalar multiplication by elements in some field. The addition and multiplication operations together give A the structure of a ring; the addition and scalar multiplication operations together give A the structure of a vector space over K. In this article we will also use the term K-algebra to mean an associative algebra over the field K. A standard first example of a K-algebra is a ring of square matrices over a field K, with the usual matrix multiplication.
In mathematical analysis and in probability theory, a σ-algebra on a set X is a collection Σ of subsets of X that
includes X itself, is closed under complement, and is closed under countable unions.
In topology and related branches of mathematics, a topological space may be defined as a set of points, along with a set of neighbourhoods for each point, satisfying a set of axioms relating points and neighbourhoods. The definition of a topological space relies only upon set theory and is the most general notion of a mathematical space that allows for the definition of concepts such as continuity, connectedness, and convergence. Other spaces, such as manifolds and metric spaces, are specializations of topological spaces with extra structures or constraints. Being so general, topological spaces are a central unifying notion and appear in virtually every branch of modern mathematics. The branch of mathematics that studies topological spaces in their own right is called point-set topology or general topology.
This is a glossary of some terms used in the branch of mathematics known as topology. Although there is no absolute distinction between different areas of topology, the focus here is on general topology. The following definitions are also fundamental to algebraic topology, differential topology and geometric topology.

In mathematics, and more specifically in topology, an open set is an abstract concept generalizing the idea of an open interval in the real line. The simplest example is in metric spaces, where open sets can be defined as those sets which contain a ball around each of their points ; however, an open set, in general, can be very abstract: any collection of sets can be called open, as long as the union of an arbitrary number of open sets is open, the intersection of a finite number of open sets is open, and the space itself is open. These conditions are very loose, and they allow enormous flexibility in the choice of open sets. In the two extremes, every set can be open, or no set can be open but the space itself and the empty set.

In mathematics, general topology is the branch of topology that deals with the basic set-theoretic definitions and constructions used in topology. It is the foundation of most other branches of topology, including differential topology, geometric topology, and algebraic topology. Another name for general topology is point-set topology.
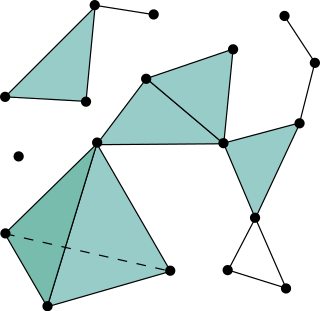
In mathematics, a simplicial complex is a set composed of points, line segments, triangles, and their n-dimensional counterparts. Simplicial complexes should not be confused with the more abstract notion of a simplicial set appearing in modern simplicial homotopy theory. The purely combinatorial counterpart to a simplicial complex is an abstract simplicial complex.
In mathematics, the Gelfand representation in functional analysis has two related meanings:
In the mathematical field of functional analysis there are several standard topologies which are given to the algebra
of bounded linear operators on a Banach space
.
In mathematics, a filtration
is an indexed set
of subobjects of a given algebraic structure
, with the index
running over some index set
that is a totally ordered set, subject to the condition that
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of how intuitive properties of size of a set sum when considering multiple object, e.g. two apples are twice as much fruit as one apple. Additivity is a weaker condition than σ-additivity, and σ-additivity implies additivity.
In mathematics, specifically in algebraic topology, the Eilenberg–Zilber theorem is an important result in establishing the link between the homology groups of a product space
and those of the spaces
and
. The theorem first appeared in a 1953 paper in the American Journal of Mathematics by Samuel Eilenberg and J. A. Zilber. One possible route to a proof is the acyclic model theorem.
Discrete Morse theory is a combinatorial adaptation of Morse theory developed by Robin Forman. The theory has various practical applications in diverse fields of applied mathematics and computer science, such as configuration spaces, homology computation, denoising, mesh compression, and topological data analysis.
In topology, a branch of mathematics, a collapse reduces a simplicial complex to a homotopy-equivalent subcomplex. Collapses, like CW complexes themselves, were invented by J. H. C. Whitehead. Collapses find applications in computational homology.
In mathematics, lifting theory was first introduced by John von Neumann in his (1931) pioneering paper, followed later by Dorothy Maharam’s (1958) paper, and by A. Ionescu Tulcea and C. Ionescu Tulcea’s (1961) paper. Lifting theory was motivated to a large extent by its striking applications; for its development up to 1969, see the Ionescu Tulceas' work and the monograph, now a standard reference in the field. Lifting theory continued to develop after 1969, yielding significant new results and applications.
A pseudomanifold is a special type of topological space.
It looks like a manifold at most of the points, but may contain singularities.
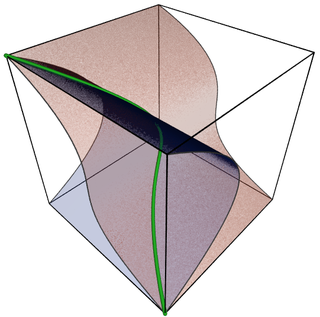
For example, the cone of solutions of
forms a pseudomanifold.
In mathematics, and especially topology, a Poincaré complex is an abstraction of the singular chain complex of a closed, orientable manifold.
In mathematics, a linear map is a mapping V → W between two modules that preserves the operations of addition and scalar multiplication.
In the theory of C*-algebras, the universal representation of a C*-algebra is a faithful representation which is the direct sum of the GNS representations corresponding to the states of the C*-algebra. The various properties of the universal representation are used to obtain information about the ideals and quotients of the C*-algebra. The close relationship between an arbitrary representation of a C*-algebra and its universal representation can be exploited to obtain several criteria for determining whether a linear functional on the algebra is ultraweakly continuous. The method of using the properties of the universal representation as a tool to prove results about the C*-algebra and its representations is commonly referred to as universal representation techniques in the literature.