
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).

Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics." Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers, or defined as generalizations of the integers.

A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1). For example, (3, 4, 5) is a primitive Pythagorean triple whereas (6, 8, 10) is not. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.
In algebra, a quadratic equation is any equation that can be rearranged in standard form as

In mathematics, a square root of a number x is a number y such that ; in other words, a number y whose square is x. For example, 4 and −4 are square roots of 16 because .
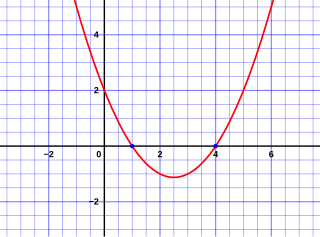
In elementary algebra, the quadratic formula is a formula that provides the two solutions, or roots, to a quadratic equation. There are other ways of solving a quadratic equation instead of using the quadratic formula, such as completing the square.
Sexagesimal, also known as base 60, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinates.

The square root of 2 is a positive real number that, when multiplied by itself, equals the number 2. It may be written in mathematics as or . It is an algebraic number, and therefore not a transcendental number. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property.
In mathematics, an algebraic equation or polynomial equation is an equation of the form , where P is a polynomial with coefficients in some field, often the field of the rational numbers. For example, is an algebraic equation with integer coefficients and
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics, important contributions were made by scholars like Aryabhata, Brahmagupta, Bhaskara II, and Varāhamihira. The decimal number system in use today was first recorded in Indian mathematics. Indian mathematicians made early contributions to the study of the concept of zero as a number, negative numbers, arithmetic, and algebra. In addition, trigonometry was further advanced in India, and, in particular, the modern definitions of sine and cosine were developed there. These mathematical concepts were transmitted to the Middle East, China, and Europe and led to further developments that now form the foundations of many areas of mathematics.
Methods of computing square roots are algorithms for approximating the non-negative square root of a positive real number . Since all square roots of natural numbers, other than of perfect squares, are irrational, square roots can usually only be computed to some finite precision: these methods typically construct a series of increasingly accurate approximations.

Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University. This tablet, believed to have been written about 1800 BC, has a table of four columns and 15 rows of numbers in the cuneiform script of the period.

Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 602 = 3600 = 48 × 75, so as divisors of a power of 60 both 48 and 75 are regular.

Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as Al-Khwarizmi and Abu al-Wafa. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beginning with 17th-century mathematics and reaching its modern form with Leonhard Euler (1748).
Algebra can essentially be considered as doing computations similar to those of arithmetic but with non-numerical mathematical objects. However, until the 19th century, algebra consisted essentially of the theory of equations. For example, the fundamental theorem of algebra belongs to the theory of equations and is not, nowadays, considered as belonging to algebra.

YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest known computational accuracy ... in the ancient world". The tablet is believed to be the work of a student in southern Mesopotamia from some time between 1800 and 1600 BC.

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
South and West Asia consists of a wide region extending from the present-day country of Turkey in the west to Bangladesh and India in the east.
A mathematical constant is a key number whose value is fixed by an unambiguous definition, often referred to by a special symbol, or by mathematicians' names to facilitate using it across multiple mathematical problems. Constants arise in many areas of mathematics, with constants such as e and π occurring in such diverse contexts as geometry, number theory, statistics, and calculus.

IM 67118, also known as Db2-146, is an Old Babylonian clay tablet in the collection of the National Museum of Iraq that contains the solution to a problem in plane geometry concerning a rectangle with given area and diagonal. In the last part of the text, the solution is proved correct using the Pythagorean theorem. The steps of the solution are believed to represent cut-and-paste geometry operations involving a diagram from which, it has been suggested, ancient Mesopotamians might, at an earlier time, have derived the Pythagorean theorem.



























