Related Research Articles
In mathematics, a bilinear map is a function combining elements of two vector spaces to yield an element of a third vector space, and is linear in each of its arguments. Matrix multiplication is an example.

George Bernard Dantzig was an American mathematical scientist who made contributions to industrial engineering, operations research, computer science, economics, and statistics.
Antisymmetric or skew-symmetric may refer to:

In mathematical physics, Minkowski space is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be an immediate consequence of the postulates of special relativity.
In mathematics, a set of simultaneous equations, also known as a system of equations or an equation system, is a finite set of equations for which common solutions are sought. An equation system is usually classified in the same manner as single equations, namely as a:
In mathematics, a quadratic form is a polynomial with terms all of degree two. For example,
In mathematics, a sesquilinear form is a generalization of a bilinear form that, in turn, is a generalization of the concept of the dot product of Euclidean space. A bilinear form is linear in each of its arguments, but a sesquilinear form allows one of the arguments to be "twisted" in a semilinear manner, thus the name; which originates from the Latin numerical prefix sesqui- meaning "one and a half". The basic concept of the dot product – producing a scalar from a pair of vectors – can be generalized by allowing a broader range of scalar values and, perhaps simultaneously, by widening the definition of what a vector is.

A Mathematical Programming Language (AMPL) is an algebraic modeling language to describe and solve high-complexity problems for large-scale mathematical computing . It was developed by Robert Fourer, David Gay, and Brian Kernighan at Bell Laboratories. AMPL supports dozens of solvers, both open source and commercial software, including CBC, CPLEX, FortMP, Gurobi, MINOS, IPOPT, SNOPT, KNITRO, and LGO. Problems are passed to solvers as nl files. AMPL is used by more than 100 corporate clients, and by government agencies and academic institutions.
In mathematics, in the area of numerical analysis, Galerkin methods are a class of methods for converting a continuous operator problem to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a weak formulation. Typically one then applies some constraints on the function space to characterize the space with a finite set of basis functions.

In computer graphics and digital imaging, imagescaling refers to the resizing of a digital image. In video technology, the magnification of digital material is known as upscaling or resolution enhancement.
In mathematics, positive definiteness is a property of any object to which a bilinear form or a sesquilinear form may be naturally associated, which is positive definite. See, in particular:
Weak formulations are important tools for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations. In a weak formulation, an equation is no longer required to hold absolutely and has instead weak solutions only with respect to certain "test vectors" or "test functions". This is equivalent to formulating the problem to require a solution in the sense of a distribution.
In mathematics, the Cartan–Dieudonné theorem, named after Élie Cartan and Jean Dieudonné, establishes that every orthogonal transformation in an n-dimensional symmetric bilinear space can be described as the composition of at most n reflections.
In mathematics, more specifically in multilinear algebra, an alternating multilinear map is a multilinear map with all arguments belonging to the same space that is zero whenever any two adjacent arguments are equal.
The TOMLAB Optimization Environment is a modeling platform for solving applied optimization problems in MATLAB.
In mathematics, the Babuška–Lax–Milgram theorem is a generalization of the famous Lax–Milgram theorem, which gives conditions under which a bilinear form can be "inverted" to show the existence and uniqueness of a weak solution to a given boundary value problem. The result is named after the mathematicians Ivo Babuška, Peter Lax and Arthur Milgram.
nl is a file format for presenting and archiving mathematical programming problems. Initially this format has been invented for connecting solvers to AMPL. It has also been adopted by other systems such as COIN-OR, FortSP, and Coopr.
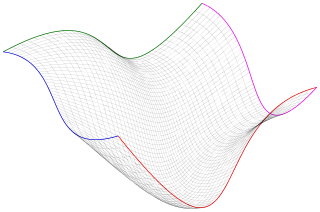
In mathematics, a Coons patch, is a type of manifold parametrization used in computer graphics to smoothly join other surfaces together, and in computational mechanics applications, particularly in finite element method and boundary element method, to mesh problem domains into elements.
References
- Bilinear program at the Mathematical Programming Glossary.
| This applied mathematics-related article is a stub. You can help Wikipedia by expanding it. |