Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves which do not share a common component. The theorem states that the number of common points of two such curves is at most equal to the product of their degrees, and equality holds if one counts points at infinity and points with complex coordinates, and if each point is counted with its intersection multiplicity. It is named after Étienne Bézout.
The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.

In mathematics, a plane real algebraic curve is the set of points on the Euclidean plane whose coordinates are zeros of some polynomial in two variables. More generally an algebraic curve is similar but may be embedded in a higher dimensional space or defined over some more general field.
In algebraic geometry and computational geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible, which is referred to as special position. Its precise meaning differs in different settings.

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge (Συναγωγή) or Collection, and for Pappus's hexagon theorem in projective geometry. Nothing is known of his life, other than, that he had a son named Hermodorus, and was a teacher in Alexandria.

Pierre Ossian Bonnet was a French mathematician. He made some important contributions to the differential geometry of surfaces, including the Gauss–Bonnet theorem.
In mathematics, the canonical bundle of a non-singular algebraic variety of dimension over a field is the line bundle , which is the nth exterior power of the cotangent bundle Ω on V.
A porism is a mathematical proposition or corollary. In particular, the term porism has been used to refer to a direct result of a proof, analogous to how a corollary refers to a direct result of a theorem. In modern usage, a porism is a relation that holds for an infinite range of values but only if a certain condition is assumed, for example Steiner's porism. The term originates from three books of Euclid with porism, that have been lost. Note that a proposition may not have been proven, so a porism may not be a theorem, or for that matter, it may not be true.
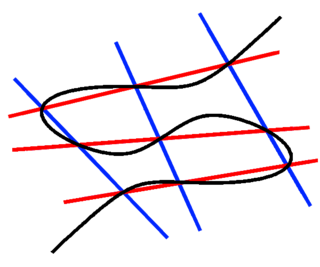
In mathematics, the Cayley–Bacharach theorem is a statement about cubic curves in the projective plane P2. The original form states:
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.
Chasles' theorem may refer to any of several mathematical results attributed to Michel Chasles (1793–1880):
In algebraic geometry, a field of mathematics, the AF+BG theorem is a result of Max Noether which describes when the equation of an algebraic curve in the complex projective plane can be written in terms of the equations of two other algebraic curves.

In mathematics, Cramer's paradox or the Cramer–Euler paradox is the statement that the number of points of intersection of two higher-order curves in the plane can be greater than the number of arbitrary points that are usually needed to define one such curve. It is named after the Genevan mathematician Gabriel Cramer.
In algebraic geometry, a branch of mathematics, the Lefschetz theorem on (1,1)-classes, named after Solomon Lefschetz, is a classical statement relating holomorphic line bundles on a compact Kähler manifold to classes in its integral cohomology. It is the only case of the Hodge conjecture which has been proved for all Kähler manifolds.
In Euclidean and projective geometry, just as two (distinct) points determine a line, five points determine a conic. There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.
In algebraic geometry, the Chasles–Cayley–Brill formula states that a correspondence T of valence k from an algebraic curve C of genus g to itself has d + e + 2kg united points, where d and e are the degrees of T and its inverse.
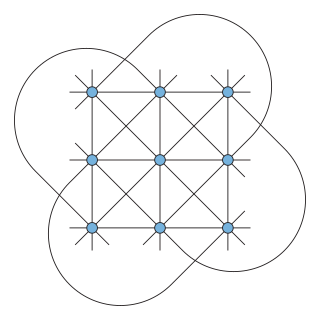
In geometry, the Hesse configuration, introduced by Colin Maclaurin and studied by Hesse (1844), is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane.

In kinematics, Chasles' theorem, or Mozzi–Chasles' theorem, says that the most general rigid body displacement can be produced by a translation along a line followed by a rotation about an axis parallel to that line.
In gravitation, Chasles' theorem says that the Newtonian gravitational attraction of a spherical shell, outside of that shell, is equivalent mathematically to the attraction of a point mass.









