Related Research Articles

The decimal numeral system is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as decimal notation.

In computing, floating-point arithmetic (FP) is arithmetic that represents subsets of real numbers using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. Numbers of this form are called floating-point numbers. For example, 12.345 is a floating-point number in base ten with five digits of precision:
IEEE 754-1985 is a historic industry standard for representing floating-point numbers in computers, officially adopted in 1985 and superseded in 2008 by IEEE 754-2008, and then again in 2019 by minor revision IEEE 754-2019. During its 23 years, it was the most widely used format for floating-point computation. It was implemented in software, in the form of floating-point libraries, and in hardware, in the instructions of many CPUs and FPUs. The first integrated circuit to implement the draft of what was to become IEEE 754-1985 was the Intel 8087.
A computer number format is the internal representation of numeric values in digital device hardware and software, such as in programmable computers and calculators. Numerical values are stored as groupings of bits, such as bytes and words. The encoding between numerical values and bit patterns is chosen for convenience of the operation of the computer; the encoding used by the computer's instruction set generally requires conversion for external use, such as for printing and display. Different types of processors may have different internal representations of numerical values and different conventions are used for integer and real numbers. Most calculations are carried out with number formats that fit into a processor register, but some software systems allow representation of arbitrarily large numbers using multiple words of memory.
Double-precision floating-point format is a floating-point number format, usually occupying 64 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point.
A real data type is a data type used in a computer program to represent an approximation of a real number. Because the real numbers are not countable, computers cannot represent them exactly using a finite amount of information. Most often, a computer will use a rational approximation to a real number.
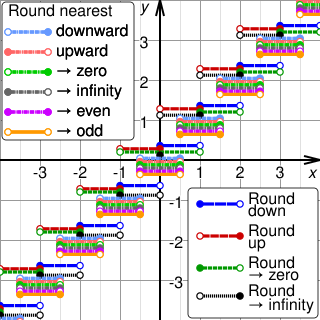
Rounding or rounding off means replacing a number with an approximate value that has a shorter, simpler, or more explicit representation. For example, replacing $23.4476 with $23.45, the fraction 312/937 with 1/3, or the expression √2 with 1.414.
In computer science, primitive data types are a set of basic data types from which all other data types are constructed. Specifically it often refers to the limited set of data representations in use by a particular processor, which all compiled programs must use. Most processors support a similar set of primitive data types, although the specific representations vary. More generally, "primitive data types" may refer to the standard data types built into a programming language. Data types which are not primitive are referred to as derived or composite.
The IEEE Standard for Floating-Point Arithmetic is a technical standard for floating-point arithmetic established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating-point implementations that made them difficult to use reliably and portably. Many hardware floating-point units use the IEEE 754 standard.
The significand refers to the first (left) part of a number in scientific notation or related concepts in floating-point representation, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.
In computing, fixed-point is a method of representing fractional (non-integer) numbers by storing a fixed number of digits of their fractional part. Dollar amounts, for example, are often stored with exactly two fractional digits, representing the cents. More generally, the term may refer to representing fractional values as integer multiples of some fixed small unit, e.g. a fractional amount of hours as an integer multiple of ten-minute intervals. Fixed-point number representation is often contrasted to the more complicated and computationally demanding floating-point representation.
In computer science, arbitrary-precision arithmetic, also called bignum arithmetic, multiple-precision arithmetic, or sometimes infinite-precision arithmetic, indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most arithmetic logic unit (ALU) hardware, which typically offers between 8 and 64 bits of precision.
In computer science, a scale factor is a number used as a multiplier to represent a number on a different scale, functioning similarly to an exponent in mathematics. A scale factor is used when a real-world set of numbers needs to be represented on a different scale in order to fit a specific number format. Although using a scale factor extends the range of representable values, it also decreases the precision, resulting in rounding error for certain calculations.
The Q notation is a way to specify the parameters of a binary fixed point number format. For example, in Q notation, the number format denoted by Q8.8 means that the fixed point numbers in this format have 8 bits for the integer part and 8 bits for the fraction part.
Extended precision refers to floating-point number formats that provide greater precision than the basic floating-point formats. Extended precision formats support a basic format by minimizing roundoff and overflow errors in intermediate values of expressions on the base format. In contrast to extended precision, arbitrary-precision arithmetic refers to implementations of much larger numeric types using special software.
The IEEE 754-2008 standard includes decimal floating-point number formats in which the significand and the exponent can be encoded in two ways, referred to as binary encoding and decimal encoding.
IEEE 754-2008 is a revision of the IEEE 754 standard for floating-point arithmetic. It was published in August 2008 and is a significant revision to, and replaces, the IEEE 754-1985 standard. The 2008 revision extended the previous standard where it was necessary, added decimal arithmetic and formats, tightened up certain areas of the original standard which were left undefined, and merged in IEEE 854 . In a few cases, where stricter definitions of binary floating-point arithmetic might be performance-incompatible with some existing implementation, they were made optional. In 2019, it was updated with a minor revision IEEE 754-2019.
Some programming languages provide a built-in (primitive) rational data type to represent rational numbers like 1/3 and -11/17 without rounding, and to do arithmetic on them. Examples are the ratio type of Common Lisp, and analogous types provided by most languages for algebraic computation, such as Mathematica and Maple. Many languages that do not have a built-in rational type still provide it as a library-defined type.
Single-precision floating-point format is a computer number format, usually occupying 32 bits in computer memory; it represents a wide dynamic range of numeric values by using a floating radix point.
References
- ↑ "Floating-point numeric types - C# reference".
- ↑ "Decimal — Decimal fixed point and floating point arithmetic — Python 3.10.0 documentation".
- ↑ "Data management". IBM .
- ↑ "How the new ABAP Data Type DECFLOAT helps computing complex calculation? « SAP Ignite". Archived from the original on 2012-08-09. Retrieved 2012-07-28.
- ↑ "GCC Manual". 6.13 Decimal Floating Types.