
In geometry, a hexagon is a six-sided polygon or 6-gon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
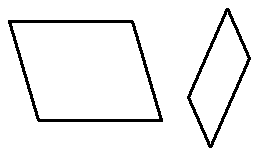
Traditionally, in two-dimensional geometry, a rhomboid is a parallelogram in which adjacent sides are of unequal lengths and angles are non-right angled.
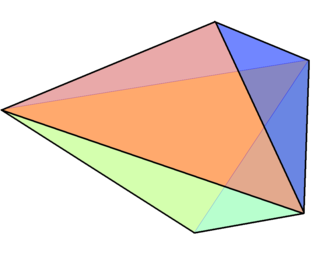
In geometry, the triangular bipyramid is a type of hexahedron, being the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.

In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has C4v symmetry. If all edges are equal, it is an equilateral square pyramid, the Johnson solid J1.

In chemistry, trigonal planar is a molecular geometry model with one atom at the center and three atoms at the corners of an equilateral triangle, called peripheral atoms, all in one plane. In an ideal trigonal planar species, all three ligands are identical and all bond angles are 120°. Such species belong to the point group D3h. Molecules where the three ligands are not identical, such as H2CO, deviate from this idealized geometry. Examples of molecules with trigonal planar geometry include boron trifluoride (BF3), formaldehyde (H2CO), phosgene (COCl2), and sulfur trioxide (SO3). Some ions with trigonal planar geometry include nitrate (NO−
3), carbonate (CO2−
3), and guanidinium (C(NH
2)+
3). In organic chemistry, planar, three-connected carbon centers that are trigonal planar are often described as having sp2 hybridization.

In Euclidean geometry, an equiangular polygon is a polygon whose vertex angles are equal. If the lengths of the sides are also equal then it is a regular polygon. Isogonal polygons are equiangular polygons which alternate two edge lengths.

In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.

In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It is also known as an anticube.
In geometry, the gyroelongated bipyramids are an infinite set of polyhedra, constructed by elongating an n-gonal bipyramid by inserting an n-gonal antiprism between its congruent halves.
In geometry, a polytope, or a tiling, is isotoxal or edge-transitive if its symmetries act transitively on its edges. Informally, this means that there is only one type of edge to the object: given two edges, there is a translation, rotation and/or reflection that will move one edge to the other, while leaving the region occupied by the object unchanged.

In geometry, the sphinx tiling is a tessellation of the plane using the "sphinx", a pentagonal hexiamond formed by gluing six equilateral triangles together. The resultant shape is named for its reminiscence to the Great Sphinx at Giza. A sphinx can be dissected into any square number of copies of itself, some of them mirror images, and repeating this process leads to a non-periodic tiling of the plane. The sphinx is therefore a rep-tile. It is one of few known pentagonal rep-tiles and is the only known pentagonal rep-tile whose sub-copies are equal in size.

In geometry, a rotunda is any member of a family of dihedral-symmetric polyhedra. They are similar to a cupola but instead of alternating squares and triangles, it alternates pentagons and triangles around an axis. The pentagonal rotunda is a Johnson solid.
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers.

In geometry, the snub pentapentagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of sr{5,5}, constructed from two regular pentagons and three equilateral triangles around every vertex.

In geometry, the snub heptaheptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of sr{7,7}, constructed from two regular heptagons and three equilateral triangles around every vertex.

In geometry, the snub apeiroapeirogonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of s{∞,∞}. It has 3 equilateral triangles and 2 apeirogons around every vertex, with vertex figure 3.3.∞.3.∞.

In geometry, a diminished trapezohedron is a polyhedron in an infinite set of polyhedra, constructed by removing one of the polar vertices of a trapezohedron and replacing it by a new face (diminishment). It has one regular n-gonal base face, n triangles faces around the base, and n kites meeting on top. The kites can also be replaced by rhombi with specific proportions.

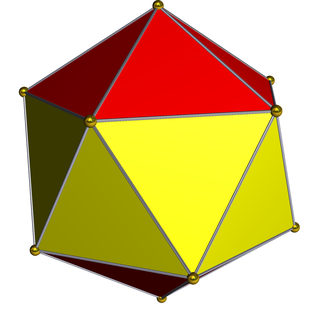
In geometry, an icosahedron is a polyhedron with 20 faces. The name comes from Ancient Greek εἴκοσι (eíkosi), meaning 'twenty', and ἕδρα (hédra), meaning 'seat'. The plural can be either "icosahedra" or "icosahedrons".
















