In linguistics, homonyms, broadly defined, are words which sound alike or are spelled alike, but have different meanings. A more restrictive definition sees homonyms as words that are simultaneously homographs and homophones – that is to say they have identical pronunciation and spelling, whilst maintaining different meanings. The relationship between a set of homonyms is called homonymy. Examples of homonyms are the pair stalk and stalk and the pair left and left. A distinction is sometimes made between true homonyms, which are unrelated in origin, such as skate and skate, and polysemous homonyms, or polysemes, which have a shared origin, such as mouth and mouth.

A homophone is a word that is pronounced the same as another word but differs in meaning. A homophone may also differ in spelling. The two words may be spelled the same, such as rose (flower) and rose, or differently, such as carat, and carrot, or to, two, and too. The term "homophone" may also apply to units longer or shorter than words, such as phrases, letters, or groups of letters which are pronounced the same as another phrase, letter, or group of letters. Any unit with this property is said to be "homophonous".
In mathematics, a projective line is, roughly speaking, the extension of a usual line by a point called a point at infinity. The statement and the proof of many theorems of geometry are simplified by the resultant elimination of special cases; for example, two distinct projective lines in a projective plane meet in exactly one point.
In mathematics, a linear fractional transformation is, roughly speaking, a transformation of the form
In mathematics, the Cayley transform, named after Arthur Cayley, is any of a cluster of related things. As originally described by Cayley (1846), the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. The transform is a homography used in real analysis, complex analysis, and quaternionic analysis. In the theory of Hilbert spaces, the Cayley transform is a mapping between linear operators.
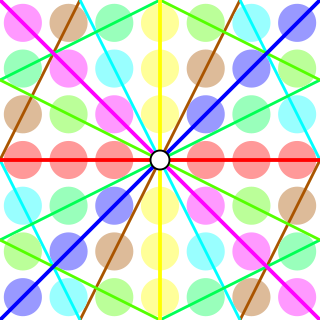
In mathematics, the projective line over a ring is an extension of the concept of projective line over a field. Given a ring A with 1, the projective line P(A) over A consists of points identified by homogeneous coordinates. Let U be the group of units of A; pairs (a,b) and (c,d) from A × A are related when there is a u in U such that ua = c and ub = d. This relation is an equivalence relation. A typical equivalence class is written U(a,b).

Bruges is a commune in the Gironde department in Nouvelle-Aquitaine in southwestern
France, just north of Bordeaux.
Image stitching or photo stitching is the process of combining multiple photographic images with overlapping fields of view to produce a segmented panorama or high-resolution image. Commonly performed through the use of computer software, most approaches to image stitching require nearly exact overlaps between images and identical exposures to produce seamless results, although some stitching algorithms actually benefit from differently exposed images by doing high-dynamic-range-imaging in regions of overlap. Some digital cameras can stitch their photos internally.
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. A collineation is thus an isomorphism between projective spaces, or an automorphism from a projective space to itself. Some authors restrict the definition of collineation to the case where it is an automorphism. The set of all collineations of a space to itself form a group, called the collineation group.

Image rectification is a transformation process used to project images onto a common image plane. This process has several degrees of freedom and there are many strategies for transforming images to the common plane.
In mathematics, quaternionic analysis is the study of functions with quaternions as the domain and/or range. Such functions can be called functions of a quaternion variable just as functions of a real variable or a complex variable are called.

In projective geometry, a special conformal transformation is a linear fractional transformation that is not an affine transformation. Thus the generation of a special conformal transformation involves use of multiplicative inversion, which is the generator of linear fractional transformations that is not affine.

In geometry, a W-curve is a curve in projective n-space that is invariant under a 1-parameter group of projective transformations. W-curves were first investigated by Felix Klein and Sophus Lie in 1871, who also named them. W-curves in the real projective plane can be constructed with straightedge alone. Many well-known curves are W-curves, among them conics, logarithmic spirals, powers (like y = x3), logarithms and the helix, but not e.g. the sine. W-curves occur widely in the realm of plants.

Kig is free and open-source interactive geometry software, which is part of the KDE Education Project. It has some facilities for scripting in Python, as well as the creating macros from existing constructions.

In geometry, a real projective line is an extension of the usual concept of line that has been historically introduced to solve a problem set by visual perspective: two parallel lines do not intersect but seem to intersect "at infinity". For solving this problem, points at infinity have been introduced, in such a way that in a real projective plane, two distinct projective lines meet in exactly one point. The set of these points at infinity, the "horizon" of the visual perspective in the plane, is a real projective line. It is the circle of directions emanating from an observer situated at any point, with opposite points identified. A model of the real projective line is the projectively extended real line. Drawing a line to represent the horizon in visual perspective, an additional point at infinity is added to represent the collection of lines parallel to the horizon.
An interlingual homograph is a word that occurs in more than one written language, but which has a different meaning or pronunciation in each language.







