In mathematics, particularly in algebra, a field extension is a pair of fields such that the operations of E are those of F restricted to E. In this case, F is an extension field of E and E is a subfield of F. For example, under the usual notions of addition and multiplication, the complex numbers are an extension field of the real numbers; the real numbers are a subfield of the complex numbers.

In mathematics, a polynomial is an expression consisting of indeterminates and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponentiation of variables. An example of a polynomial of a single indeterminate x is x2 − 4x + 7. An example in three variables is x3 + 2xyz2 − yz + 1.

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. In other words, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
In mathematics, the discriminant of a polynomial is a quantity that depends on the coefficients and determines various properties of the roots. It is generally defined as a polynomial function of the coefficients of the original polynomial. The discriminant is widely used in polynomial factoring, number theory, and algebraic geometry. It is often denoted by the symbol .
In mathematics, and specially in algebra, a formal series is an infinite sum that is considered independently from any notion of convergence, and can be manipulated with the usual algebraic operations on series.
Bézout's theorem is a statement in algebraic geometry concerning the number of common zeros of n polynomials in n indeterminates. In its original form the theorem states that in general the number of common zeros equals the product of the degrees of the polynomials. It is named after Étienne Bézout.

In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation that accepts a function and returns another function.
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring K[x1, …, xn] over a field K. A Gröbner basis allows many important properties of the ideal and the associated algebraic variety to be deduced easily, such as the dimension and the number of zeros when it is finite. Gröbner basis computation is one of the main practical tools for solving systems of polynomial equations and computing the images of algebraic varieties under projections or rational maps.
In mathematics, a monomial is, roughly speaking, a polynomial which has only one term. Two definitions of a monomial may be encountered:
- A monomial, also called power product, is a product of powers of variables with nonnegative integer exponents, or, in other words, a product of variables, possibly with repetitions. For example, is a monomial. The constant is a monomial, being equal to the empty product and to for any variable . If only a single variable is considered, this means that a monomial is either or a power of , with a positive integer. If several variables are considered, say, then each can be given an exponent, so that any monomial is of the form with non-negative integers.
- A monomial is a monomial in the first sense multiplied by a nonzero constant, called the coefficient of the monomial. A monomial in the first sense is a special case of a monomial in the second sense, where the coefficient is . For example, in this interpretation and are monomials.
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity. This ring serves as universal structure in which relations between symmetric polynomials can be expressed in a way independent of the number n of indeterminates. Among other things, this ring plays an important role in the representation theory of the symmetric group.

In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates with coefficients in another ring, often a field.
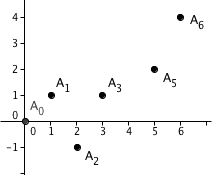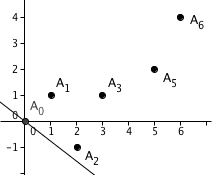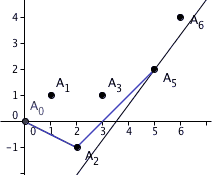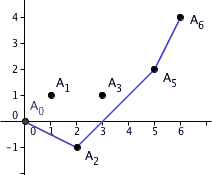
In mathematics, the Newton polygon is a tool for understanding the behaviour of polynomials over local fields.
In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function.
In mathematics, the resultant of two polynomials is a polynomial expression of their coefficients, which is equal to zero if and only if the polynomials have a common root, or, equivalently, a common factor. In some older texts, the resultant is also called the eliminant.
In mathematics, a variable is a symbol and placeholder for (historically) a quantity that may change, or (nowadays) any mathematical object. In particular, a variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set.
In mathematics, in particular in algebra, polarization is a technique for expressing a homogeneous polynomial in a simpler fashion by adjoining more variables. Specifically, given a homogeneous polynomial, polarization produces a multilinear form from which the original polynomial can be recovered by evaluating along a certain diagonal.
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the rationals, but not over the integers.
In ring theory, a branch of mathematics, a ring R is a polynomial identity ring if there is, for some N > 0, an element P ≠ 0 of the free algebra, Z⟨X1, X2, ..., XN⟩, over the ring of integers in N variables X1, X2, ..., XN such that
In algebra and in particular in algebraic combinatorics, a quasisymmetric function is any element in the ring of quasisymmetric functions which is in turn a subring of the formal power series ring with a countable number of variables. This ring generalizes the ring of symmetric functions. This ring can be realized as a specific limit of the rings of quasisymmetric polynomials in n variables, as n goes to infinity. This ring serves as universal structure in which relations between quasisymmetric polynomials can be expressed in a way independent of the number n of variables.
In algebraic geometry, the main theorem of elimination theory states that every projective scheme is proper. A version of this theorem predates the existence of scheme theory. It can be stated, proved, and applied in the following more classical setting. Let k be a field, denote by the n-dimensional projective space over k. The main theorem of elimination theory is the statement that for any n and any algebraic variety V defined over k, the projection map sends Zariski-closed subsets to Zariski-closed subsets.


























