
The Fresnel equations describe the reflection and transmission of light when incident on an interface between different optical media. They were deduced by Augustin-Jean Fresnel who was the first to understand that light is a transverse wave, even though no one realized that the "vibrations" of the wave were electric and magnetic fields. For the first time, polarization could be understood quantitatively, as Fresnel's equations correctly predicted the differing behaviour of waves of the s and p polarizations incident upon a material interface.

The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength λ (lambda) and time period T as

In physics, mathematics, and related fields, a wave is a disturbance of a field in which a physical attribute oscillates repeatedly at each point or propagates from each point to neighboring points, or seems to move through space.
The amplitude of a periodic variable is a measure of its change over a single period. There are various definitions of amplitude, which are all functions of the magnitude of the difference between the variable's extreme values. In older texts the phase is sometimes called the amplitude.

Polarization is a property applying to transverse waves that specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. A simple example of a polarized transverse wave is vibrations traveling along a taut string (see image); for example, in a musical instrument like a guitar string. Depending on how the string is plucked, the vibrations can be in a vertical direction, horizontal direction, or at any angle perpendicular to the string. In contrast, in longitudinal waves, such as sound waves in a liquid or gas, the displacement of the particles in the oscillation is always in the direction of propagation, so these waves do not exhibit polarization. Transverse waves that exhibit polarization include electromagnetic waves such as light and radio waves, gravitational waves, and transverse sound waves in solids. In some types of transverse waves, the wave displacement is limited to a single direction, so these also do not exhibit polarization; for example, in surface waves in liquids, the wave displacement of the particles is always in a vertical plane.

A transverse wave is a moving wave that consists of oscillations that are perpendicular to the direction of propagation of the wave.

Seismic waves are waves of energy that travel through the Earth's layers, and are a result of earthquakes, volcanic eruptions, magma movement, large landslides and large man-made explosions that give out low-frequency acoustic energy. Many other natural and anthropogenic sources create low-amplitude waves commonly referred to as ambient vibrations. Seismic waves are studied by geophysicists called seismologists. Seismic wave fields are recorded by a seismometer, hydrophone, or accelerometer.

Longitudinal waves are waves in which the displacement of the medium is in the same direction as, or the opposite direction to, the direction of propagation of the wave. Mechanical longitudinal waves are also called compressional or compression waves, because they produce compression and rarefaction when traveling through a medium, and pressure waves, because they produce increases and decreases in pressure.

A sine wave or sinusoid is a mathematical curve that describes a smooth periodic oscillation. A sine wave is a continuous wave. It is named after the function sine, of which it is the graph. It occurs often in pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. Its most basic form as a function of time (t) is:

Reflection is the change in direction of a wavefront at an interface between two different media so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves. The law of reflection says that for specular reflection the angle at which the wave is incident on the surface equals the angle at which it is reflected. Mirrors exhibit specular reflection.

Reflection seismology is a method of exploration geophysics that uses the principles of seismology to estimate the properties of the Earth's subsurface from reflected seismic waves. The method requires a controlled seismic source of energy, such as dynamite or Tovex blast, a specialized air gun or a seismic vibrator, commonly known by the trademark name Vibroseis. Reflection seismology is similar to sonar and echolocation. This article is about surface seismic surveys; for vertical seismic profiles, see VSP.

In geophysics and reflection seismology, amplitude versus offset (AVO) or amplitude variation with offset is the general term for referring to the dependency of the seismic attribute, amplitude, with the distance between the source and receiver. AVO analysis is a technique that geophysicists can execute on seismic data to determine a rock’s fluid content, porosity, density or seismic velocity, shear wave information, fluid indicators.
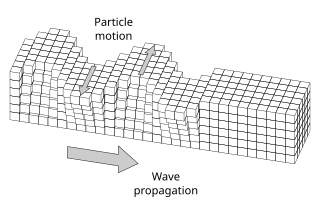
In elastodynamics, Love waves, named after Augustus Edward Hough Love, are horizontally polarized surface waves. The Love wave is a result of the interference of many shear waves (S–waves) guided by an elastic layer, which is welded to an elastic half space on one side while bordering a vacuum on the other side. In seismology, Love waves are surface seismic waves that cause horizontal shifting of the Earth during an earthquake. Augustus Edward Hough Love predicted the existence of Love waves mathematically in 1911. They form a distinct class, different from other types of seismic waves, such as P-waves and S-waves, or Rayleigh waves. Love waves travel with a lower velocity than P- or S- waves, but faster than Rayleigh waves. These waves are observed only when there is a low velocity layer overlying a high velocity layer/ sub–layers.
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces, complicating analysis. Ray tracing solves the problem by repeatedly advancing idealized narrow beams called rays through the medium by discrete amounts. Simple problems can be analyzed by propagating a few rays using simple mathematics. More detailed analysis can be performed by using a computer to propagate many rays.
The surface wave magnitude scale is one of the magnitude scales used in seismology to describe the size of an earthquake. It is based on measurements in Rayleigh surface waves that travel primarily along the uppermost layers of the Earth. It is currently used in People's Republic of China as a national standard for categorising earthquakes.
Coronal seismology is a technique of studying the plasma of the Sun's corona with the use of magnetohydrodynamic (MHD) waves and oscillations. Magnetohydrodynamics studies the dynamics of electrically conducting fluids - in this case the fluid is the coronal plasma. Observed properties of the waves (e.g. period, wavelength, amplitude, temporal and spatial signatures, characteristic scenarios of the wave evolution, combined with a theoretical modelling of the wave phenomena, may reflect physical parameters of the corona which are not accessible in situ, such as the coronal magnetic field strength and Alfvén velocity and coronal dissipative coefficients. Originally, the method of MHD coronal seismology was suggested by Y. Uchida in 1970 for propagating waves, and B. Roberts et al. in 1984 for standing waves, but was not practically applied until the late 90s due to a lack of necessary observational resolution. Philosophically, coronal seismology is similar to the Earth's seismology, helioseismology, and MHD spectroscopy of laboratory plasma devices. In all these approaches, waves of various kind are used to probe a medium.

Karl Bernhard Zoeppritz was a German geophysicist who made important contributions to seismology, in particular the formulation of the Zoeppritz equations.
Seismic site effects are related to the amplification of seismic waves in superficial geological layers. The surface ground motion may be strongly amplified if the geological conditions are unfavorable. Therefore, the study of local site effects is an important part of the assessment of strong ground motions, seismic hazard and engineering seismology in general. Damage due to an earthquake may thus be aggravated as in the case of the 1985 Mexico City earthquake. For alluvial basins, we may shake a bowl of jelly to model the phenomenon at a small scale.















