This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
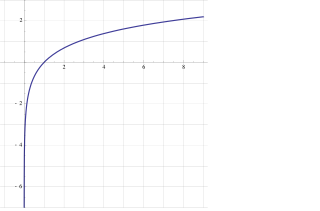
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, loge x, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x) or log(x). This is done in particular when the argument to the logarithm is not a single symbol, to prevent ambiguity.
An order of magnitude is an approximate measure of the number of digits that a number has in the commonly-used base-ten number system. It is equal to the whole number floor of logarithm (base 10). For example, the order of magnitude of 1500 is 3, because 1500 = 1.5 × 103.
The neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. The unit's name is derived from the name of John Napier, the inventor of logarithms. As is the case for the decibel and bel, the neper is a unit defined in the international standard ISO 80000. It is not part of the International System of Units (SI), but is accepted for use alongside the SI.
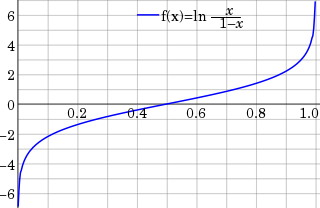
In statistics, the logit function or the log-odds is the logarithm of the odds p/(1 − p) where p is the probability.. It is a type of function that creates a map of probability values from
to
. It is the inverse of the sigmoidal "logistic" function or logistic transform used in mathematics, especially in statistics.

Mathematical tables are lists of numbers showing the results of calculation with varying arguments. Before calculators were cheap and plentiful, people would use such tables to simplify and drastically speed up computation. Tables of logarithms and trigonometric functions were common in math and science textbooks. Specialized tables were published for applications such as astronomy, celestial navigation and statistics.

In mathematics, the binary logarithm is the power to which the number 2 must be raised to obtain the value n. That is, for any real number x,
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formula
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point. Multi-valued functions are rigorously studied using Riemann surfaces, and the formal definition of branch points employs this concept.
This is a list of logarithm topics, by Wikipedia page. See also the list of exponential topics.
In mathematics, a closed-form expression is a mathematical expression that can be evaluated in a finite number of operations. It may contain constants, variables, certain "well-known" operations, and functions, but usually no limit. The set of operations and functions admitted in a closed-form expression may vary with author and context.

The term Napierian logarithm or Naperian logarithm, named after John Napier, is often used to mean the natural logarithm. Napier did not introduce this natural logarithmic function, although it is named after him. However, if it is taken to mean the "logarithms" as originally produced by Napier, it is a function given by :
In convex analysis, a non-negative function f : Rn → R+ is logarithmically concave if its domain is a convex set, and if it satisfies the inequality
In probability theory and computer science, a log probability is simply a logarithm of a probability. The use of log probabilities means representing probabilities on a logarithmic scale, instead of the standard
unit interval.

In mathematics, logarithmic growth describes a phenomenon whose size or cost can be described as a logarithm function of some input. e.g. y = C log (x). Note that any logarithm base can be used, since one can be converted to another by multiplying by a fixed constant. Logarithmic growth is the inverse of exponential growth and is very slow.
A logarithmic number system (LNS) is an arithmetic system used for representing real numbers in computer and digital hardware, especially for digital signal processing.
In mathematics, the super-logarithm is one of the two inverse functions of tetration. Just as exponentiation has two inverse functions, roots and logarithms, tetration has two inverse functions, super-roots and super-logarithms. There are several ways of interpreting super-logarithms:
In calculus, logarithmic differentiation or differentiation by taking logarithms is a method used to differentiate functions by employing the logarithmic derivative of a function f,