| Look up logistic in Wiktionary, the free dictionary. |
Logistic may refer to:
| Look up logistic in Wiktionary, the free dictionary. |
Logistic may refer to:
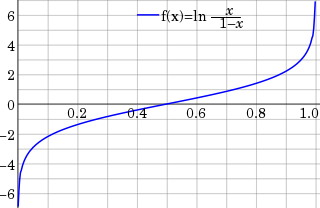
In statistics, the logit function or the log-odds is the logarithm of the odds p/(1 − p) where p is the probability.. It is a type of function that creates a map of probability values from to . It is the inverse of the sigmoidal "logistic" function or logistic transform used in mathematics, especially in statistics.
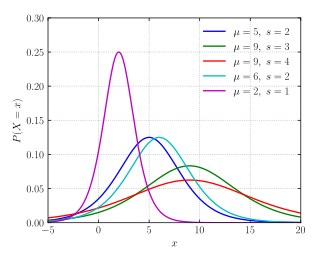
In probability theory and statistics, the logistic distribution is a continuous probability distribution. Its cumulative distribution function is the logistic function, which appears in logistic regression and feedforward neural networks. It resembles the normal distribution in shape but has heavier tails. The logistic distribution is a special case of the Tukey lambda distribution.

A logistic function or logistic curve is a common "S" shape, with equation:
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation first created by Pierre François Verhulst. Mathematically, the logistic map is written

In statistics, the logistic model is a widely used statistical model. In its basic form it uses a logistic function to model a binary dependent variable, although many more complex extensions exist. In regression analysis, logistic regression is estimating the parameters of a logistic model. Mathematically, a binary logistic model has a dependent variable with two possible values, such as pass/fail, win/lose, alive/dead or healthy/sick; these are represented by an indicator variable, where the two values are labeled "0" and "1". In the logistic model, the log-odds for the value labeled "1" is a linear combination of one or more independent variables ("predictors"); the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. Analogous models with a different sigmoid function instead of the logistic function can also be used, such as the probit model; the defining characteristic of the logistic model is that increasing one of the independent variables multiplicatively scales the odds of the given outcome at a constant rate, with each dependent variable having its own parameter; for a binary independent variable this generalizes the odds ratio.

Logistics is generally the detailed organization and implementation of a complex operation. In a general business sense, logistics is the management of the flow of things between the point of origin and the point of consumption in order to meet requirements of customers or corporations. The resources managed in logistics may include tangible goods such as materials, equipment, and supplies, as well as food and other consumable items. The logistics of physical items usually involves the integration of information flow, materials handling, production, packaging, inventory, transportation, warehousing, and often security.

Military logistics is the discipline of planning and carrying out the movement and maintenance of military forces. In its most comprehensive sense, it is those aspects or military operations that deal with:
| This disambiguation page lists articles associated with the title Logistic. If an internal link led you here, you may wish to change the link to point directly to the intended article. |

Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not vary smoothly in this way, but have distinct, separated values. Discrete mathematics therefore excludes topics in "continuous mathematics" such as calculus or Euclidean geometry. Discrete objects can often be enumerated by integers. More formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics." Indeed, discrete mathematics is described less by what is included than by what is excluded: continuously varying quantities and related notions.
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of these outcomes is called an event.
Statistics is a field of inquiry that studies the collection, analysis, interpretation, and presentation of data. It is applicable to a wide variety of academic disciplines, from the physical and social sciences to the humanities; it is also used and misused for making informed decisions in all areas of business and government.
Fuzzy logic is a form of many-valued logic in which the truth values of variables may be any real number between 0 and 1 inclusive. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.

A sigmoid function is a mathematical function having a characteristic "S"-shaped curve or sigmoid curve. Often, sigmoid function refers to the special case of the logistic function shown in the first figure and defined by the formula

In probability theory and statistics, the Gumbel distribution is used to model the distribution of the maximum of a number of samples of various distributions. This distribution might be used to represent the distribution of the maximum level of a river in a particular year if there was a list of maximum values for the past ten years. It is useful in predicting the chance that an extreme earthquake, flood or other natural disaster will occur. The potential applicability of the Gumbel distribution to represent the distribution of maxima relates to extreme value theory, which indicates that it is likely to be useful if the distribution of the underlying sample data is of the normal or exponential type. The rest of this article refers to the Gumbel distribution to model the distribution of the maximum value. To model the minimum value, use the negative of the original values.
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not vary smoothly in this way, but have distinct, separated values. Discrete mathematics therefore excludes topics in "continuous mathematics" such as calculus and analysis.
This article itemizes the various lists of mathematics topics. Some of these lists link to hundreds of articles; some link only to a few. The template to the right includes links to alphabetical lists of all mathematical articles. This article brings together the same content organized in a manner better suited for browsing.

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory.
In probability theory, especially in mathematical statistics, a location–scale family is a family of probability distributions parametrized by a location parameter and a non-negative scale parameter. For any random variable whose probability distribution function belongs to such a family, the distribution function of also belongs to the family. Moreover, if and are two random variables whose distribution functions are members of the family, and assuming 1) existence of the first two moments and 2) has zero mean and unit variance, then can be written as , where and are the mean and standard deviation of .
Logic is the formal science of using reason and is considered a branch of both philosophy and mathematics. Logic investigates and classifies the structure of statements and arguments, both through the study of formal systems of inference and the study of arguments in natural language. The scope of logic can therefore be very large, ranging from core topics such as the study of fallacies and paradoxes, to specialized analyses of reasoning such as probability, correct reasoning, and arguments involving causality. One of the aims of logic is to identify the correct and incorrect inferences. Logicians study the criteria for the evaluation of arguments.
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive beyond any given specified time.
Probability distribution fitting or simply distribution fitting is the fitting of a probability distribution to a series of data concerning the repeated measurement of a variable phenomenon.