The fundamental frequency, often referred to simply as the fundamental, is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In terms of a superposition of sinusoids, the fundamental frequency is the lowest frequency sinusoidal in the sum. In some contexts, the fundamental is usually abbreviated as f0, indicating the lowest frequency counting from zero. In other contexts, it is more common to abbreviate it as f1, the first harmonic.
Since the fundamental is the lowest frequency and is also perceived as the loudest, the ear identifies it as the specific pitch of the musical tone [harmonic spectrum]....The individual partials are not heard separately but are blended together by the ear into a single tone.

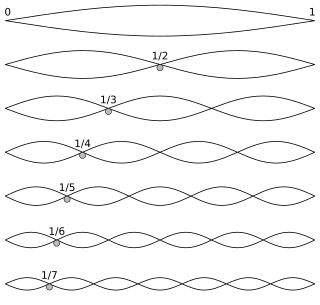
A harmonic series is the sequence of sounds—pure tones, represented by sinusoidal waves—in which the frequency of each sound is an integer multiple of the fundamental, the lowest frequency.

The pitch of a brass instrument is determined by its vibratory length, which determines the fundamental frequency of the open instrument and the frequencies of its overtones. Additional pitches are achieved by varying the length using the instrument's valve, slide, key or crook system. The fundamental frequency is not playable on some brass instruments. The table provides the pitch of the second overtone and length for some common brass instruments in descending order of pitch. This pitch is notated transpositionally as middle C for many of these brass instruments.

A crystal oscillator is an electronic oscillator circuit that uses the mechanical resonance of a vibrating crystal of piezoelectric material to create an electrical signal with a precise frequency. This frequency is often used to keep track of time, as in quartz wristwatches, to provide a stable clock signal for digital integrated circuits, and to stabilize frequencies for radio transmitters and receivers. The most common type of piezoelectric resonator used is the quartz crystal, so oscillator circuits incorporating them became known as crystal oscillators, but other piezoelectric materials including polycrystalline ceramics are used in similar circuits.
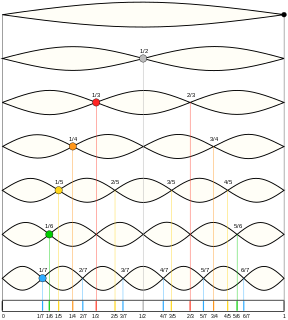
A harmonic is any member of the harmonic series. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. It is typically applied to repeating signals, such as sinusoidal waves. A harmonic of such a wave is a wave with a frequency that is a positive integer multiple of the frequency of the original wave, known as the fundamental frequency. The original wave is also called the 1st harmonic, the following harmonics are known as higher harmonics. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz, 150 Hz, 200 Hz and any addition of waves with these frequencies is periodic at 50 Hz.
An nth characteristic mode, for n > 1, will have nodes that are not vibrating. For example, the 3rd characteristic mode will have nodes at L and L, where L is the length of the string. In fact, each nth characteristic mode, for n not a multiple of 3, will not have nodes at these points. These other characteristic modes will be vibrating at the positions L and L. If the player gently touches one of these positions, then these other characteristic modes will be suppressed. The tonal harmonics from these other characteristic modes will then also be suppressed. Consequently, the tonal harmonics from the nth characteristic modes, where n is a multiple of 3, will be made relatively more prominent.

An overtone is any frequency greater than the fundamental frequency of a sound. Using the model of Fourier analysis, the fundamental and the overtones together are called partials. Harmonics, or more precisely, harmonic partials, are partials whose frequencies are numerical integer multiples of the fundamental. These overlapping terms are variously used when discussing the acoustic behavior of musical instruments. The model of Fourier analysis provides for the inclusion of inharmonic partials, which are partials whose frequencies are not whole-number ratios of the fundamental.

Overtone singing – also known as overtone chanting, harmonic singing, or throat singing – is a type of singing in which the singer manipulates the resonances created in the vocal tract, in order to produce a melody.

Pitch is a perceptual property of sounds that allows their ordering on a frequency-related scale, or more commonly, pitch is the quality that makes it possible to judge sounds as "higher" and "lower" in the sense associated with musical melodies. Pitch can be determined only in sounds that have a frequency that is clear and stable enough to distinguish from noise. Pitch is a major auditory attribute of musical tones, along with duration, loudness, and timbre.

A harmonic sound is said to have a missing fundamental, suppressed fundamental, or phantom fundamental when its overtones suggest a fundamental frequency but the sound lacks a component at the fundamental frequency itself. The brain perceives the pitch of a tone not only by its fundamental frequency, but also by the periodicity implied by the relationship between the higher harmonics; we may perceive the same pitch even if the fundamental frequency is missing from a tone.
Piano acoustics are the physical properties of the piano that affect its sound.
Undertone or Undertones may refer to:
Musical acoustics or music acoustics is a multidisciplinary field that combines knowledge from physics, psychophysics, organology, physiology, music theory, ethnomusicology, signal processing and instrument building, among other disciplines. As a branch of acoustics, it is concerned with researching and describing the physics of music – how sounds are employed to make music. Examples of areas of study are the function of musical instruments, the human voice, computer analysis of melody, and in the clinical use of music in music therapy.
A person who is specialized in the making of stringed instruments such as guitars, lutes and violins is called a luthier.
Harmonic usually refers to the frequency components of a time-varying signal, such as a musical note.
In music, the undertone series or subharmonic series is a sequence of notes that results from inverting the intervals of the overtone series. While overtones naturally occur with the physical production of music on instruments, undertones must be produced in unusual ways. While the overtone series is based upon arithmetic multiplication of frequencies, resulting in a harmonic series, the undertone series is based on arithmetic division.

A string harmonic is a string instrument technique which uses the nodes of natural harmonics of a musical string to produce high pitched tones of varying timbre and loudness. String harmonics are "high pitched tones, like a whistle's, are produced when the musician lightly touches certain points on a string." "A flute-like sound produced on a string instrument by lightly touching the string with the finger instead of pressing it down," against the fingerboard.

The Moodswinger is a twelve-string electric zither with an additional third bridge designed by Yuri Landman. The rod which functions as the third bridge divides the strings into two sections to cause an overtone multiphonic sound. One of the copies of the instrument is part of the collection of the Musical Instrument Museum in Phoenix, Arizona.

In music, klang is a term sometimes used to translate the German Klang, a highly polysemic word. Technically, the term denotes any periodic sound, especially as opposed to simple periodic sounds. In the German lay usage, it may mean "sound" or "tone", "musical tone", "note", or "timbre"; a chord of three notes is called a Dreiklang, etc.
In vibrational spectroscopy, an overtone band is the spectral band that occurs in a vibrational spectrum of a molecule when the molecule makes a transition from the ground state (v=0) to the second excited state (v=2), where v is the vibrational quantum number obtained from solving the Schrödinger equation for the molecule.

Among alternative tunings for the guitar, an overtones tuning selects its open-string notes from the overtone sequence of a fundamental note. An example is the open tuning constituted by the first six overtones of the fundamental note C, namely C2-C3-G3-C4-E4-G4.










