Pierpont prime

Pierpont prime
Named after	James Pierpont
No. of known terms	Thousands
Conjectured no. of terms	Infinite
Subsequence of	Pierpont number
First terms	2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889
Largest known term	81 × 220,498,148 + 1
OEIS index	A005109

Last updated October 23, 2023

In number theory, a Pierpont prime is a prime number of the form

for some nonnegative integers $u$ and $v$ . That is, they are the prime numbers $p$ for which $p - 1$ is 3-smooth. They are named after the mathematician James Pierpont, who used them to characterize the regular polygons that can be constructed using conic sections. The same characterization applies to polygons that can be constructed using ruler, compass, and angle trisector, or using paper folding.

Except for 2 and the Fermat primes, every Pierpont prime must be 1 modulo 6. The first few Pierpont primes are:

2, 3, 5, 7, 13, 17, 19, 37, 73, 97, 109, 163, 193, 257, 433, 487, 577, 769, 1153, 1297, 1459, 2593, 2917, 3457, 3889, 10369, 12289, 17497, 18433, 39367, 52489, 65537, 139969, 147457, 209953, 331777, 472393, 629857, 746497, 786433, 839809, 995329, ... (sequence A005109 in the OEIS)

It has been conjectured that there are infinitely many Pierpont primes, but this remains unproven.

Distribution

Unsolved problem in mathematics:

Are there infinitely many Pierpont primes?

(more unsolved problems in mathematics)

A Pierpont prime with $v = 0$ is of the form $2^{u}+1$ , and is therefore a Fermat prime (unless $u = 0$ ). If $v$ is positive then $u$ must also be positive (because $3^{v}+1$ would be an even number greater than 2 and therefore not prime), and therefore the non-Fermat Pierpont primes all have the form $6 k + 1$ , when $k$ is a positive integer (except for 2, when $u = v = 0$ ).

Empirically, the Pierpont primes do not seem to be particularly rare or sparsely distributed; there are 42 Pierpont primes less than 10⁶, 65 less than 10⁹, 157 less than 10²⁰, and 795 less than 10¹⁰⁰. There are few restrictions from algebraic factorisations on the Pierpont primes, so there are no requirements like the Mersenne prime condition that the exponent must be prime. Thus, it is expected that among $n$ -digit numbers of the correct form $2^{u}\cdot 3^{v}+1$ , the fraction of these that are prime should be proportional to $1/ n$ , a similar proportion as the proportion of prime numbers among all $n$ -digit numbers. As there are $\Theta (n^{2})$ numbers of the correct form in this range, there should be $\Theta (n)$ Pierpont primes.

Andrew M. Gleason made this reasoning explicit, conjecturing there are infinitely many Pierpont primes, and more specifically that there should be approximately $9 n$ Pierpont primes up to $10 n$ .^[1] According to Gleason's conjecture there are $\Theta (\log N)$ Pierpont primes smaller than N, as opposed to the smaller conjectural number $O(\log \log N)$ of Mersenne primes in that range.

Primality testing

When $2^{u}>3^{v}$ , $2^{u}\cdot 3^{v}+1$ is a Proth number and thus its primality can be tested by Proth's theorem. On the other hand, when $2^{u}<3^{v}$ alternative primality tests for $M=2^{u}\cdot 3^{v}+1$ are possible based on the factorization of $M-1$ as a small even number multiplied by a large power of 3.^[2]

Pierpont primes found as factors of Fermat numbers

As part of the ongoing worldwide search for factors of Fermat numbers, some Pierpont primes have been announced as factors. The following table^[3] gives values of m, k, and n such that

2^{2^{m}}+1

is divisible by

3^{k}\cdot 2^{n}+1.

The left-hand side is a Fermat number; the right-hand side is a Pierpont prime.


m	k	n	Year	Discoverer
38	1	41	1903	Cullen, Cunningham & Western
63	2	67	1956	Robinson
207	1	209	1956	Robinson
452	3	455	1956	Robinson
9428	2	9431	1983	Keller
12185	4	12189	1993	Dubner
28281	4	28285	1996	Taura
157167	1	157169	1995	Young
213319	1	213321	1996	Young
303088	1	303093	1998	Young
382447	1	382449	1999	Cosgrave & Gallot
461076	1	461081	2003	Nohara, Jobling, Woltman & Gallot
495728	5	495732	2007	Keiser, Jobling, Penné & Fougeron
672005	3	672007	2005	Cooper, Jobling, Woltman & Gallot
2145351	1	2145353	2003	Cosgrave, Jobling, Woltman & Gallot
2478782	1	2478785	2003	Cosgrave, Jobling, Woltman & Gallot
2543548	2	2543551	2011	Brown, Reynolds, Penné & Fougeron

As of 2023^[update], the largest known Pierpont prime is 81 × 2^20498148 + 1 (6,170,560 decimal digits), whose primality was discovered in June 2023.^[4]

Polygon construction

In the mathematics of paper folding, the Huzita axioms define six of the seven types of fold possible. It has been shown that these folds are sufficient to allow the construction of the points that solve any cubic equation.^[5] It follows that they allow any regular polygon of $N$ sides to be formed, as long as $N \geq 3$ and is of the form $2 m 3 n ρ$ , where $ρ$ is a product of distinct Pierpont primes. This is the same class of regular polygons as those that can be constructed with a compass, straightedge, and angle trisector.^[1] Regular polygons which can be constructed with only compass and straightedge (constructible polygons) are the special case where $n = 0$ and $ρ$ is a product of distinct Fermat primes, themselves a subset of Pierpont primes.

In 1895, James Pierpont studied the same class of regular polygons; his work is what gives the name to the Pierpont primes. Pierpont generalized compass and straightedge constructions in a different way, by adding the ability to draw conic sections whose coefficients come from previously constructed points. As he showed, the regular $N$ -gons that can be constructed with these operations are the ones such that the totient of $N$ is 3-smooth. Since the totient of a prime is formed by subtracting one from it, the primes $N$ for which Pierpont's construction works are exactly the Pierpont primes. However, Pierpont did not describe the form of the composite numbers with 3-smooth totients.^[6] As Gleason later showed, these numbers are exactly the ones of the form $2 m 3 n ρ$ given above.^[1]

The smallest prime that is not a Pierpont (or Fermat) prime is 11; therefore, the hendecagon is the first regular polygon that cannot be constructed with compass, straightedge and angle trisector (or origami, or conic sections). All other regular $N$ -gons with $3 \leq N \leq 21$ can be constructed with compass, straightedge and trisector.^[1]

Generalization

A Pierpont prime of the second kind is a prime number of the form 2^u3^v − 1. These numbers are

2, 3, 5, 7, 11, 17, 23, 31, 47, 53, 71, 107, 127, 191, 383, 431, 647, 863, 971, 1151, 2591, 4373, 6143, 6911, 8191, 8747, 13121, 15551, 23327, 27647, 62207, 73727, 131071, 139967, 165887, 294911, 314927, 442367, 472391, 497663, 524287, 786431, 995327, ... (sequence A005105 in the OEIS)

The largest known primes of this type are Mersenne primes; currently the largest known is $2^{82589933}-1$ (24,862,048 decimal digits). The largest known Pierpont prime of the second kind that is not a Mersenne prime is $3\cdot 2^{20928756}-1$ , found by PrimeGrid.^[7]

A generalized Pierpont prime is a prime of the form $p_{1}^{n_{1}}\!\cdot p_{2}^{n_{2}}\!\cdot p_{3}^{n_{3}}\!\cdot \ldots \cdot p_{k}^{n_{k}}+1$ with k fixed primes p₁ < p₂ < p₃ < ... < p_k. A generalized Pierpont prime of the second kind is a prime of the form $p_{1}^{n_{1}}\!\cdot p_{2}^{n_{2}}\!\cdot p_{3}^{n_{3}}\!\cdot \ldots \cdot p_{k}^{n_{k}}-1$ with k fixed primes p₁ < p₂ < p₃ < ... < p_k. Since all primes greater than 2 are odd, in both kinds p₁ must be 2. The sequences of such primes in the OEIS are:

{p₁, p₂, p₃, ..., p_k}	+ 1	− 1
{2}	OEIS: A092506	OEIS: A000668
{2, 3}	OEIS: A005109	OEIS: A005105
{2, 5}	OEIS: A077497	OEIS: A077313
{2, 3, 5}	OEIS: A002200	OEIS: A293194
{2, 7}	OEIS: A077498	OEIS: A077314
{2, 3, 5, 7}	OEIS: A174144	OEIS: A347977
{2, 11}	OEIS: A077499	OEIS: A077315
{2, 13}	OEIS: A173236	OEIS: A173062

Related Research Articles

In geometry and algebra, a real number $is constructible if and only if, given a line segment of unit length, a line segment of length can be constructed with compass and straightedge in a finite number of steps. Equivalently, is constructible if and only if there is a closed-form expression for using only integers and the operations for addition, subtraction, multiplication, division, and square roots.$

<span class="mw-page-title-main">Prime number</span> Number divisible only by 1 or itself

A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.

<span class="mw-page-title-main">Straightedge and compass construction</span> Method of drawing geometric objects

In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.

2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.

<span class="mw-page-title-main">Angle trisection</span> Construction of an angle equal to one third a given angle

Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

In mathematics, a Fermat number, named after Pierre de Fermat, the first known to have studied them, is a positive integer of the form

11 (eleven) is the natural number following 10 and preceding 12. It is the first repdigit. In English, it is the smallest positive integer whose name has three syllables.

The Huzita–Justin axioms or Huzita–Hatori axioms are a set of rules related to the mathematical principles of origami, describing the operations that can be made when folding a piece of paper. The axioms assume that the operations are completed on a plane, and that all folds are linear. These are not a minimal set of axioms but rather the complete set of possible single folds.

In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

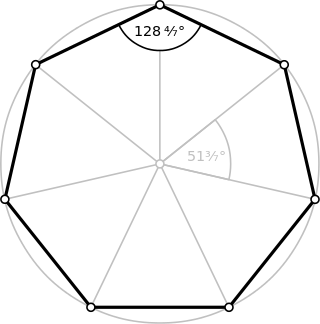
In geometry, a heptagon or septagon is a seven-sided polygon or 7-gon.

31 (thirty-one) is the natural number following 30 and preceding 32. It is a prime number.

<span class="mw-page-title-main">Constructible polygon</span> Regular polygon that can be constructed with compass and straightedge

In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not. There are infinitely many constructible polygons, but only 31 with an odd number of sides are known.

In geometry, a hendecagon or 11-gon is an eleven-sided polygon.

In geometry, a tridecagon or triskaidecagon or 13-gon is a thirteen-sided polygon.

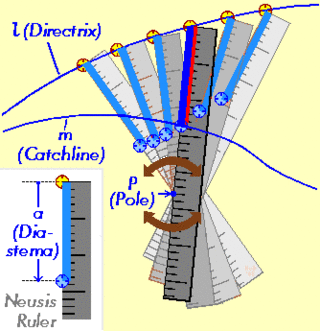
In geometry, the neusis is a geometric construction method that was used in antiquity by Greek mathematicians.

The number 4,294,967,295 is a whole number equal to 2³² − 1. It is a perfect totient number, meaning it is equal to the sum of its iterated totients. It follows 4,294,967,294 and precedes 4,294,967,296. It has a factorization of $.$

In number theory, a cyclotomic field is a number field obtained by adjoining a complex root of unity to $Q$ , the field of rational numbers.

In geometry, an icositrigon or 23-gon is a 23-sided polygon. The icositrigon has the distinction of being the smallest regular polygon that is not neusis constructible.

A Proth number is a natural number N of the form $where k and n are positive integers, k is odd and . A Proth prime is a Proth number that is prime. They are named after the French mathematician François Proth. The first few Proth primes are$

Geometric Origami is a book on the mathematics of paper folding, focusing on the ability to simulate and extend classical straightedge and compass constructions using origami. It was written by Austrian mathematician Robert Geretschläger and published by Arbelos Publishing in 2008. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.

References

1 2 3 4 Gleason, Andrew M. (1988), "Angle trisection, the heptagon, and the triskaidecagon", American Mathematical Monthly , 95 (3): 185–194, doi:10.2307/2323624, MR 0935432 . Footnote 8, p. 191.
↑ Kirfel, Christoph; Rødseth, Øystein J. (2001), "On the primality of $2h\cdot 3^{n}+1$ ", Discrete Mathematics , 241 (1–3): 395–406, doi:10.1016/S0012-365X(01)00125-X, MR 1861431 .
↑ Wilfrid Keller, Fermat factoring status.
↑ Caldwell, Chris, "The largest known primes", The Prime Pages , retrieved 17 June 2023; "The Prime Database: 81*2^20498148+1", The Prime Pages , retrieved 17 June 2023
↑ Hull, Thomas C. (2011), "Solving cubics with creases: the work of Beloch and Lill", American Mathematical Monthly , 118 (4): 307–315, doi:10.4169/amer.math.monthly.118.04.307, MR 2800341 .
↑ Pierpont, James (1895), "On an undemonstrated theorem of the Disquisitiones Arithmeticæ", Bulletin of the American Mathematical Society , 2 (3): 77–83, doi: 10.1090/S0002-9904-1895-00317-1 , MR 1557414 .
↑ 3*2^20928756 - 1 (6,300,184 Decimal Digits), from The Prime Pages.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[g98-1] 1 2 3 4 Gleason, Andrew M. (1988), "Angle trisection, the heptagon, and the triskaidecagon", American Mathematical Monthly , 95 (3): 185–194, doi:10.2307/2323624, MR 0935432 . Footnote 8, p. 191.

[2] Kirfel, Christoph; Rødseth, Øystein J. (2001), "On the primality of $2h\cdot 3^{n}+1$ ", Discrete Mathematics , 241 (1–3): 395–406, doi:10.1016/S0012-365X(01)00125-X, MR 1861431 .

[3] Wilfrid Keller, Fermat factoring status.

[4] Caldwell, Chris, "The largest known primes", The Prime Pages , retrieved 17 June 2023; "The Prime Database: 81*2^20498148+1", The Prime Pages , retrieved 17 June 2023

[5] Hull, Thomas C. (2011), "Solving cubics with creases: the work of Beloch and Lill", American Mathematical Monthly , 118 (4): 307–315, doi:10.4169/amer.math.monthly.118.04.307, MR 2800341 .

[6] Pierpont, James (1895), "On an undemonstrated theorem of the Disquisitiones Arithmeticæ", Bulletin of the American Mathematical Society , 2 (3): 77–83, doi: 10.1090/S0002-9904-1895-00317-1 , MR 1557414 .

[7] 3*2^20928756 - 1 (6,300,184 Decimal Digits), from The Prime Pages.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

v t e Prime number classes
By formula	Fermat ( $2 2 n + 1$ ) Mersenne ( $2 p - 1$ ) Double Mersenne ( $2 2 p -1 - 1$ ) Wagstaff $(2 p + 1)/3$ Proth ( $k \cdot2 n + 1$ ) Factorial ( $n! \pm 1$ ) Primorial ( $p n # \pm 1$ ) Euclid ( $p n # + 1$ ) Pythagorean ( $4 n + 1$ ) Pierpont ( $2 m \cdot3 n + 1$ ) Quartan ( $x 4 + y 4$ ) Solinas ( $2 m \pm 2 n \pm 1$ ) Cullen ( $n \cdot2 n + 1$ ) Woodall ( $n \cdot2 n - 1$ ) Cuban ( $x 3 - y 3)/(x - y$ ) Leyland ( $x y + y x$ ) Thabit ( $3\cdot2 n - 1$ ) Williams ( $(b -1)\cdot b n - 1$ ) Mills ( $⌊ A 3 n ⌋$ )
By integer sequence	Fibonacci Lucas Pell Newman–Shanks–Williams Perrin Partitions Bell Motzkin
By property	Wieferich (pair) Wall–Sun–Sun Wolstenholme Wilson Lucky Fortunate Ramanujan Pillai Regular Strong Stern Supersingular (elliptic curve) Supersingular (moonshine theory) Good Super Higgs Highly cototient Unique
Base-dependent	Palindromic Emirp Repunit $(10 n - 1)/9$ Permutable Circular Truncatable Minimal Delicate Primeval Full reptend Unique Happy Self Smarandache–Wellin Strobogrammatic Dihedral Tetradic
Patterns	Twin ( $p, p + 2$ ) Bi-twin chain ( $n \pm 1, 2 n \pm 1, 4 n \pm 1, \dots$ ) Triplet ( $p, p + 2 or p + 4, p + 6$ ) Quadruplet ( $p, p + 2, p + 6, p + 8$ ) k-tuple Cousin ( $p, p + 4$ ) Sexy ( $p, p + 6$ ) Chen Sophie Germain/Safe ( $p, 2 p + 1$ ) Cunningham ( $p, 2 p \pm 1, 4 p \pm 3, 8 p \pm 7, ...$ ) Arithmetic progression ( $p + a\cdotn, n = 0, 1, 2, 3, ...$ ) Balanced ( $consecutive p - n, p, p + n$ )
By size	Mega (1,000,000+ digits) Largest known list
Complex numbers	Eisenstein prime Gaussian prime
Composite numbers	Pseudoprime Catalan Elliptic Euler Euler–Jacobi Fermat Frobenius Lucas Somer–Lucas Strong Carmichael number Almost prime Semiprime Sphenic number Interprime Pernicious
Related topics	Probable prime Industrial-grade prime Illegal prime Formula for primes Prime gap
First 60 primes	2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281
List of prime numbers