Biostatistics are the application of statistics to a wide range of topics in biology. It encompasses the design of biological experiments, especially in medicine, pharmacy, agriculture and fishery; the collection, summarization, and analysis of data from those experiments; and the interpretation of, and inference from, the results. A major branch is medical biostatistics, which is exclusively concerned with medicine and health.
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that satisfy the basic principles stated for these different approaches. Within a given approach, statistical theory gives ways of comparing statistical procedures; it can find a best possible procedure within a given context for given statistical problems, or can provide guidance on the choice between alternative procedures.
Statistics is a field of inquiry that studies the collection, analysis, interpretation, and presentation of data. It is applicable to a wide variety of academic disciplines, from the physical and social sciences to the humanities; it is also used and misused for making informed decisions in all areas of business and government.
A statistical hypothesis, sometimes called confirmatory data analysis, is a hypothesis that is testable on the basis of observing a process that is modeled via a set of random variables. A statistical hypothesis test is a method of statistical inference. Commonly, two statistical data sets are compared, or a data set obtained by sampling is compared against a synthetic data set from an idealized model. A hypothesis is proposed for the statistical relationship between the two data sets, and this is compared as an alternative to an idealized null hypothesis that proposes no relationship between two data sets. The comparison is deemed statistically significant if the relationship between the data sets would be an unlikely realization of the null hypothesis according to a threshold probability—the significance level. Hypothesis tests are used in determining what outcomes of a study would lead to a rejection of the null hypothesis for a pre-specified level of significance. The process of distinguishing between the null hypothesis and the alternative hypothesis is aided by identifying two conceptual types of errors. The first type occurs when the null hypothesis is falsely rejected. The second type of error occurs when the null hypothesis is falsely assumed to be true. By specifying a threshold probability ('alpha') on, e.g., the admissible risk of making a type 1 error, the statistical decision process can be controlled.
In statistics, family-wise error rate (FWER) is the probability of making one or more false discoveries, or type I errors when performing multiple hypotheses tests.
In statistical hypothesis testing, a type I error is the rejection of a true null hypothesis, while a type II error is the failure to reject a false null hypothesis. More simply stated, a type I error is to falsely infer the existence of something that is not there, while a type II error is to falsely infer the absence of something that is present.
Omnibus tests are a kind of statistical test. They test whether the explained variance in a set of data is significantly greater than the unexplained variance, overall. One example is the F-test in the analysis of variance. There can be legitimate significant effects within a model even if the omnibus test is not significant. For instance, in a model with two independent variables, if only one variable exerts a significant effect on the dependent variable and the other does not, then the omnibus test may be non-significant. This fact does not affect the conclusions that may be drawn from the one significant variable. In order to test effects within an omnibus test, researchers often use contrasts.
In statistics, the Bonferroni correction is one of several methods used to counteract the problem of multiple comparisons.
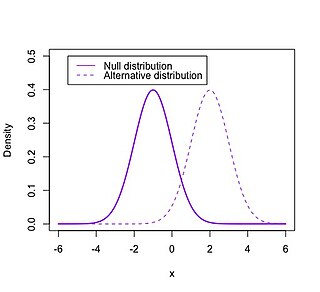
In statistical hypothesis testing, the null distribution is the probability distribution of the test statistic when the null hypothesis is true. For example, in an F-test, the null distribution is an F-distribution. Null distribution is a tool scientists often use when conducting experiments. The null distribution is the distribution of two sets of data under a null hypothesis. If the results of the two sets of data are not outside the parameters of the expected results, then the null hypothesis is said to be true.

In statistics, the multiple comparisons, multiplicity or multiple testing problem occurs when one considers a set of statistical inferences simultaneously or infers a subset of parameters selected based on the observed values. In certain fields it is known as the look-elsewhere effect.
Statistical conclusion validity is the degree to which conclusions about the relationship among variables based on the data are correct or ‘reasonable’. This began as being solely about whether the statistical conclusion about the relationship of the variables was correct, but now there is a movement towards moving to ‘reasonable’ conclusions that use: quantitative, statistical, and qualitative data. Fundamentally, two types of errors can occur: type I and type II. Statistical conclusion validity concerns the qualities of the study that make these types of errors more likely. Statistical conclusion validity involves ensuring the use of adequate sampling procedures, appropriate statistical tests, and reliable measurement procedures.
Mauchly's sphericity test is a statistical test used to validate a repeated measures analysis of variance (ANOVA).
Repeated measures design is a research design that involves multiple measures of the same variable taken on the same or matched subjects either under different conditions or over two or more time periods. For instance, repeated measurements are collected in a longitudinal study in which change over time is assessed.
In statistics, a shrinkage estimator is an estimator that, either explicitly or implicitly, incorporates the effects of shrinkage. In loose terms this means that a naive or raw estimate is improved by combining it with other information. The term relates to the notion that the improved estimate is made closer to the value supplied by the 'other information' than the raw estimate. In this sense, shrinkage is used to regularize ill-posed inference problems.
In statistics, when performing multiple comparisons, a false positive ratio is the probability of falsely rejecting the null hypothesis for a particular test. The false positive rate is calculated as the ratio between the number of negative events wrongly categorized as positive and the total number of actual negative events.
The Newman–Keuls or Student–Newman–Keuls (SNK) method is a stepwise multiple comparisons procedure used to identify sample means that are significantly different from each other. It was named after Student (1927), D. Newman, and M. Keuls. This procedure is often used as a post-hoc test whenever a significant difference between three or more sample means has been revealed by an analysis of variance (ANOVA). The Newman–Keuls method is similar to Tukey's range test as both procedures use studentized range statistics. Unlike Tukey's range test, the Newman–Keuls method uses different critical values for different pairs of mean comparisons. Thus, the procedure is more likely to reveal significant differences between group means and to commit type I errors by incorrectly rejecting a null hypothesis when it is true. In other words, the Neuman-Keuls procedure is more powerful but less conservative than Tukey's range test.
In statistics, one purpose for the analysis of variance (ANOVA) is to analyze differences in means between groups. The test statistic, F, assumes independence of observations, homogeneous variances, and population normality. ANOVA on ranks is a statistic designed for situations when the normality assumption has been violated.
In statistics, a false coverage rate (FCR) is the average rate of false coverage, i.e. not covering the true parameters, among the selected intervals.


