In abstract algebra, the center of a group, G, is the set of elements that commute with every element of G. It is denoted Z(G), from German Zentrum, meaning center. In set-builder notation,
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.

In mathematics, given two groups, (G, ∗) and (H, ·), a group homomorphism from (G, ∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that

In mathematics, a Lie algebra is a vector space together with an operation called the Lie bracket, an alternating bilinear map , that satisfies the Jacobi identity. Otherwise said, a Lie algebra is an algebra over a field where the multiplication operation is now called Lie bracket and has two additional properties: it is alternating and satisfies the Jacobi identity. The Lie bracket of two vectors and is denoted . The Lie bracket does not need to be associative, meaning that the Lie algebra can be non associative. Given an associative algebra, a Lie bracket can be and is often defined through the commutator, namely defining correctly defines a Lie bracket in addition to the already existing multiplication operation.

In mathematics, a group is a non-empty set with an operation that satisfies the following constraints: the operation is associative, has an identity element, and every element of the set has an inverse element.

In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:
In group theory, Cayley's theorem, named in honour of Arthur Cayley, states that every group G is isomorphic to a subgroup of a symmetric group. More specifically, G is isomorphic to a subgroup of the symmetric group whose elements are the permutations of the underlying set of G. Explicitly,

In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.
In mathematics, a free abelian group is an abelian group with a basis. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis, also called an integral basis, is a subset such that every element of the group can be uniquely expressed as an integer combination of finitely many basis elements. For instance the two-dimensional integer lattice forms a free abelian group, with coordinatewise addition as its operation, and with the two points (1,0) and (0,1) as its basis. Free abelian groups have properties which make them similar to vector spaces, and may equivalently be called free-modules, the free modules over the integers. Lattice theory studies free abelian subgroups of real vector spaces. In algebraic topology, free abelian groups are used to define chain groups, and in algebraic geometry they are used to define divisors.

In mathematics, the adjoint representation of a Lie group G is a way of representing the elements of the group as linear transformations of the group's Lie algebra, considered as a vector space. For example, if G is , the Lie group of real n-by-n invertible matrices, then the adjoint representation is the group homomorphism that sends an invertible n-by-n matrix to an endomorphism of the vector space of all linear transformations of defined by: .
In algebra, a valuation is a function on a field that provides a measure of the size or multiplicity of elements of the field. It generalizes to commutative algebra the notion of size inherent in consideration of the degree of a pole or multiplicity of a zero in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic or analytic varieties in algebraic geometry. A field with a valuation on it is called a valued field.
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring, and its basis is the set of elements of the given group. As a ring, its addition law is that of the free module and its multiplication extends "by linearity" the given group law on the basis. Less formally, a group ring is a generalization of a given group, by attaching to each element of the group a "weighting factor" from a given ring.
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G in which the stabilizer subgroup of every point is trivial. Equivalently, a principal homogeneous space for a group G is a non-empty set X on which G acts freely and transitively . An analogous definition holds in other categories, where, for example,

In abstract algebra, a semiring is an algebraic structure. It is a generalization of a ring, dropping the requirement that each element must have an additive inverse. At the same time, it is a generalization of bounded distributive lattices.

In mathematics the spin group Spin(n) is a Lie group whose underlying manifold is the double cover of the special orthogonal group SO(n) = SO(n, R), such that there exists a short exact sequence of Lie groups (when n ≠ 2)
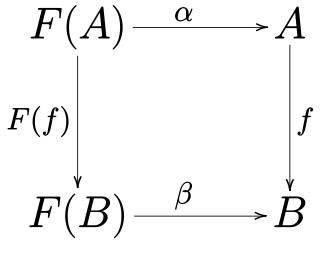
In mathematics, specifically in category theory, F-algebras generalize the notion of algebraic structure. Rewriting the algebraic laws in terms of morphisms eliminates all references to quantified elements from the axioms, and these algebraic laws may then be glued together in terms of a single functor F, the signature.
In mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.
In mathematics, the additive identity of a set that is equipped with the operation of addition is an element which, when added to any element x in the set, yields x. One of the most familiar additive identities is the number 0 from elementary mathematics, but additive identities occur in other mathematical structures where addition is defined, such as in groups and rings.

In algebra, the zero object of a given algebraic structure is, in the sense explained below, the simplest object of such structure. As a set it is a singleton, and as a magma has a trivial structure, which is also an abelian group. The aforementioned abelian group structure is usually identified as addition, and the only element is called zero, so the object itself is typically denoted as {0}. One often refers to the trivial object since every trivial object is isomorphic to any other.

In mathematics, the complexification or universal complexification of a real Lie group is given by a continuous homomorphism of the group into a complex Lie group with the universal property that every continuous homomorphism of the original group into another complex Lie group extends compatibly to a complex analytic homomorphism between the complex Lie groups. The complexification, which always exists, is unique up to unique isomorphism. Its Lie algebra is a quotient of the complexification of the Lie algebra of the original group. They are isomorphic if the original group has a quotient by a discrete normal subgroup which is linear.




















