In classical logic, disjunctive syllogism is a valid argument form which is a syllogism having a disjunctive statement for one of its premises.
First-order logic—also known as predicate logic and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects and allows the use of sentences that contain variables, so that rather than propositions such as Socrates is a man one can have expressions in the form "there exists x such that x is Socrates and x is a man" and there exists is a quantifier while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the value of the compound sentence produced depends only on that of the original sentences and on the meaning of the connective.
Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions and argument flow. Compound propositions are formed by connecting propositions by logical connectives. The propositions without logical connectives are called atomic propositions.
In logic, a many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition. Classical two-valued logic may be extended to n-valued logic for n greater than 2. Those most popular in the literature are three-valued, the finite-valued with more than three values, and the infinite-valued, such as fuzzy logic and probability logic.
In boolean logic, a disjunctive normal form (DNF) is a standardization of a logical formula which is a disjunction of conjunctive clauses; it can also be described as an OR of ANDs, a sum of products, or a cluster concept. As a normal form, it is useful in automated theorem proving.
In predicate logic, an existential quantification is a type of quantifier, a logical constant which is interpreted as "there exists", "there is at least one", or "for some". Some sources use the term existentialization to refer to existential quantification. It is usually denoted by the logical operator symbol ∃, which, when used together with a predicate variable, is called an existential quantifier. Existential quantification is distinct from universal quantification, which asserts that the property or relation holds for all members of the domain.
In mathematics, a tuple is a finite ordered list (sequence) of elements. An n-tuple is a sequence of n elements, where n is a non-negative integer. There is only one 0-tuple, an empty sequence, or empty tuple, as it is referred to. An n-tuple is defined inductively using the construction of an ordered pair.
Sequent calculus is, in essence, a style of formal logical argumentation where every line of a proof is a conditional tautology instead of an unconditional tautology. Each conditional tautology is inferred from other conditional tautologies on earlier lines in a formal argument according to rules and procedures of inference, giving a better approximation to the style of natural deduction used by mathematicians than David Hilbert's earlier style of formal logic where every line was an unconditional tautology. There may be more subtle distinctions to be made; for example, there may be non-logical axioms upon which all propositions are implicitly dependent. Then sequents signify conditional theorems in a first-order language rather than conditional tautologies.
In category theory, a subobject classifier is a special object Ω of a category such that, intuitively, the subobjects of any object X in the category correspond to the morphisms from X to Ω. In typical examples, that morphism assigns "true" to the elements of the subobject and "false" to the other elements of X. Therefore a subobject classifier is also known as a "truth value object" and the concept is widely used in the categorical description of logic. Note however that subobject classifiers are often much more complicated than the simple binary logic truth values {true, false}.
In Boolean algebra, the algebraic normal form (ANF), ring sum normal form, Zhegalkin normal form, or Reed–Muller expansion is a way of writing logical formulas in one of three subforms:
In mathematics, specifically in category theory, an -coalgebra is a structure defined according to a functor . For both algebra and coalgebra, a functor is a convenient and general way of organizing a signature. This has applications in computer science: examples of coalgebras include lazy, infinite data structures, such as streams, and also transition systems.
In mathematics, a free Boolean algebra is a Boolean algebra with a distinguished set of elements, called generators, such that:
- Each element of the Boolean algebra can be expressed as a finite combination of generators, using the Boolean operations, and
- The generators are as independent as possible, in the sense that there are no relationships among them that do not hold in every Boolean algebra no matter which elements are chosen.
In classical mechanics, holonomic constraints are relations between the position variables which can be expressed in the following form:
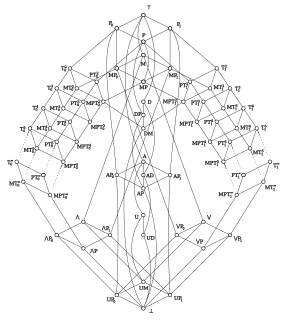
In logic and universal algebra, Post's lattice denotes the lattice of all clones on a two-element set {0, 1}, ordered by inclusion. It is named for Emil Post, who published a complete description of the lattice in 1941. The relative simplicity of Post's lattice is in stark contrast to the lattice of clones on a three-element set, which has the cardinality of the continuum, and a complicated inner structure. A modern exposition of Post's result can be found in Lau (2006).
In logic, two formulae are equisatisfiable if the first formula is satisfiable whenever the second is and vice versa; in other words, either both formulae are satisfiable or both are not. Equisatisfiable formulae may disagree, however, for a particular choice of variables. As a result, equisatisfiability is different from logical equivalence, as two equivalent formulae always have the same models.
In multilinear algebra, a reshaping is any bijective map between an order-d tensor and an order-k tensor, where k < d.
Anti-unification is the process of constructing a generalization common to two given symbolic expressions. As in unification, several frameworks are distinguished depending on which expressions are allowed, and which expressions are considered equal. If variables representing functions are allowed in an expression, the process is called "higher-order anti-unification", otherwise "first-order anti-unification". If the generalization is required to have an instance literally equal to each input expression, the process is called "syntactical anti-unification", otherwise "E-anti-unification", or "anti-unification modulo theory".
In logic, quantification specifies the quantity of specimens in the domain of discourse that satisfy an open formula. The two most common quantifiers mean "for all" and "there exists". For example, in arithmetic, quantifiers allow one to say that the natural numbers go on forever, by writing that for all n, there is another number which is one bigger than n.







