Wagner model

Last updated April 22, 2019

Wagner model is a rheological model developed for the prediction of the viscoelastic properties of polymers. It might be considered as a simplified practical form of the Bernstein-Kearsley-Zapas model. The model was developed by German rheologist Manfred Wagner.

Rheology is the study of the flow of matter, primarily in a liquid state, but also as "soft solids" or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force. It is a branch of physics which deals with the deformation and flow of materials, both solids and liquids.

Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain when stretched and immediately return to their original state once the stress is removed.

Manfred Hermann Wagner is the author of Wagner model and the molecular stress function theory for polymer rheology. He is a Professor for Polymer engineering and Polymer physics at the Technical University of Berlin.

For the isothermal conditions the model can be written as:

An isothermal process is a change of a system, in which the temperature remains constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and the change in the system will occur slowly enough to allow the system to continue to adjust to the temperature of the reservoir through heat exchange. In contrast, an adiabatic process is where a system exchanges no heat with its surroundings (Q = 0). In other words, in an isothermal process, the value ΔT = 0 and therefore the change in internal energy ΔU = 0 but Q ≠ 0, while in an adiabatic process, ΔT ≠ 0 but Q = 0.

\mathbf {\sigma } (t)=-p\mathbf {I} +\int _{-\infty }^{t}M(t-t')h(I_{1},I_{2})\mathbf {B} (t')\,dt'

where:

$\mathbf {\sigma } (t)$ is the Cauchy stress tensor as function of time t,
p is the pressure
$\mathbf {I}$ is the unity tensor
M is the memory function showing, usually expressed as a sum of exponential terms for each mode of relaxation:

In continuum mechanics, the Cauchy stress tensor $, true stress tensor, or simply called the stress tensor is a second order tensor named after Augustin-Louis Cauchy. The tensor consists of nine components that completely define the state of stress at a point inside a material in the deformed state, placement, or configuration. The tensor relates a unit-length direction vector n to the stress vector T (n) across an imaginary surface perpendicular to n :$

In the physical sciences, relaxation usually means the return of a perturbed system into equilibrium. Each relaxation process can be categorized by a relaxation time τ. The simplest theoretical description of relaxation as function of time t is an exponential law exp(-t/τ).

M(x)=\sum _{k=1}^{m}{\frac {g_{i}}{\theta _{i}}}\exp({\frac {-x}{\theta _{i}}})

, where for each mode of the relaxation,

g_{i}

is the relaxation modulus and

\theta _{i}

is the relaxation time;

$h(I_{1},I_{2})$ is the strain damping function that depends upon the first and second invariants of Finger tensor $\mathbf {B}$ .

In mathematics, in the fields of multilinear algebra and representation theory, the principal invariants of the second rank tensor $are the coefficients of the characteristic polynomial$

The strain damping function is usually written as:

h(I_{1},I_{2})=m^{*}\exp(-n_{1}{\sqrt {I_{1}-3}})+(1-m^{*})\exp(-n_{2}{\sqrt {I_{2}-3}})

,

The strain hardening function equal to one, then the deformation is small and approaching zero, then the deformations are large.

The Wagner equation can be used in the non-isothermal cases by applying time-temperature shift factor.

Related Research Articles

In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of a statistical model so the observed data is most probable. Specifically, this is done by finding the value of the parameter $that maximizes the likelihood function, which is the joint probability of the observed data, over a parameter space . The point that maximizes the likelihood function is called the maximum likelihood estimate . The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of inference within much of the quantitative research of the social and medical sciences.$

In statistics, a statistic is sufficient with respect to a statistical model and its associated unknown parameter if "no other statistic that can be calculated from the same sample provides any additional information as to the value of the parameter". In particular, a statistic is sufficient for a family of probability distributions if the sample from which it is calculated gives no additional information than does the statistic, as to which of those probability distributions is that of the population from which the sample was taken.

In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller than any relevant dimension of the body; so that its geometry and the constitutive properties of the material at each point of space can be assumed to be unchanged by the deformation.

In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:

Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of continuum mechanics. The fundamental "linearizing" assumptions of linear elasticity are: infinitesimal strains or "small" deformations and linear relationships between the components of stress and strain. In addition linear elasticity is valid only for stress states that do not produce yielding. These assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis.

In probability theory and statistics, a Gaussian process is a stochastic process, such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space.

In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman-Darmois family. The terms "distribution" and "family" are often used loosely: properly, an exponential family is a set of distributions, where the specific distribution varies with the parameter; however, a parametric family of distributions is often referred to as "a distribution", and the set of all exponential families is sometimes loosely referred to as "the" exponential family.

A Newtonian fluid is a fluid in which the viscous stresses arising from its flow, at every point, are linearly proportional to the local strain rate—the rate of change of its deformation over time. That is equivalent to saying those forces are proportional to the rates of change of the fluid's velocity vector as one moves away from the point in question in various directions.

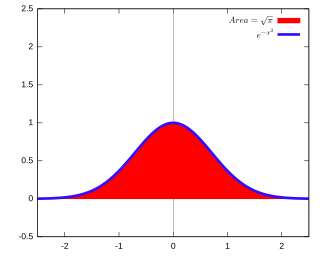
Gaussian integral Integral of the Gaussian function, equal to sqrt(π)

The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function e^−x² over the entire real line. It is named after the German mathematician Carl Friedrich Gauss. The integral is:

In mathematics, the Ornstein–Uhlenbeck process is a stochastic process with applications in financial mathematics and the physical sciences. Its original application in physics was as a model for the velocity of a massive Brownian particle under the influence of friction. It is named after Leonard Ornstein and George Eugene Uhlenbeck.

In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime. The timelike unit vector field is often denoted by $and the three spacelike unit vector fields by . All tensorial quantities defined on the manifold can be expressed using the frame field and its dual coframe field.$

The cross-entropy (CE) method is a Monte Carlo method for importance sampling and optimization. It is applicable to both combinatorial and continuous problems, with either a static or noisy objective.

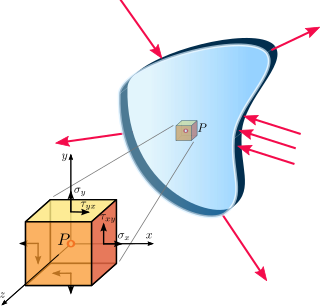
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.

In probability and statistics, a natural exponential family (NEF) is a class of probability distributions that is a special case of an exponential family (EF). Every distribution possessing a moment-generating function is a member of a natural exponential family, and the use of such distributions simplifies the theory and computation of generalized linear models.

In probability and statistics, the class of exponential dispersion models (EDM) is a set of probability distributions that represents a generalisation of the natural exponential family. Exponential dispersion models play an important role in statistical theory, in particular in generalized linear models because they have a special structure which enables deductions to be made about appropriate statistical inference.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.

Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.

In continuum mechanics, an Arruda–Boyce model is a hyperelastic constitutive model used to describe the mechanical behavior of rubber and other polymeric substances. This model is based on the statistical mechanics of a material with a cubic representative volume element containing eight chains along the diagonal directions. The material is assumed to be incompressible.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems.

In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.

References

M.H. Wagner Rheologica Acta, v.15, 136 (1976)
M.H. Wagner Rheologica Acta, v.16, 43, (1977)
B. Fan, D. Kazmer, W. Bushko, Polymer Engineering and Science, v44, N4 (2004)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.