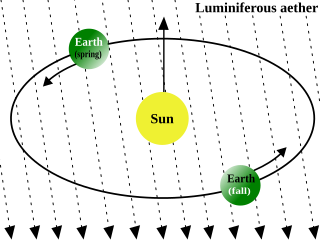
Luminiferous aether or ether, was the postulated medium for the propagation of light. It was invoked to explain the ability of the apparently wave-based light to propagate through empty space, something that waves should not be able to do. The assumption of a spatial plenum of luminiferous aether, rather than a spatial vacuum, provided the theoretical medium that was required by wave theories of light.

Mathematics includes the study of such topics as quantity, structure, space, and change.
Management science (MS) is the broad interdisciplinary study of problem solving and decision making in human organizations, with strong links to management, economics, business, engineering, management consulting, and other sciences. It uses various scientific research-based principles, strategies, and analytical methods including mathematical modeling, statistics and numerical algorithms to improve an organization's ability to enact rational and accurate management decisions by arriving at optimal or near optimal solutions to complex decision problems. Management science helps businesses to achieve goals using various scientific methods.

Quantum mechanics, including quantum field theory, is a fundamental theory in physics which describes nature at the smallest scales of energy levels of atoms and subatomic particles.

Set theory is a branch of mathematical logic that studies sets, which informally are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used to define nearly all mathematical objects.

Mathematical analysis is the branch of mathematics dealing with limits
and related theories, such as differentiation, integration, measure, infinite series, and analytic functions.

A pattern is a regularity in the world, man-made design, or abstract ideas. As such, the elements of a pattern repeat in a predictable manner. A geometric pattern is a kind of pattern formed of geometric shapes and typically repeated like a wallpaper design.
Foundations of mathematics is the study of the philosophical and logical and/or algorithmic basis of mathematics, or, in a broader sense, the mathematical investigation of what underlies the philosophical theories concerning the nature of mathematics. In this latter sense, the distinction between foundations of mathematics and philosophy of mathematics turns out to be quite vague.
Foundations of mathematics can be conceived as the study of the basic mathematical concepts and how they form hierarchies of more complex structures and concepts, especially the fundamentally important structures that form the language of mathematics also called metamathematical concepts, with an eye to the philosophical aspects and the unity of mathematics. The search for foundations of mathematics is a central question of the philosophy of mathematics; the abstract nature of mathematical objects presents special philosophical challenges.
Model, modeling or modelling may refer to:
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics. Mathematical notations include relatively simple symbolic representations, such as the numbers 0, 1 and 2; function symbols such as sin; operator symbols such as "+"; conceptual symbols such as lim and dy/dx; equations and variables; and complex diagrammatic notations such as Penrose graphical notation and Coxeter–Dynkin diagrams.

The point spread function (PSF) describes the response of an imaging system to a point source or point object. A more general term for the PSF is a system's impulse response, the PSF being the impulse response of a focused optical system. The PSF in many contexts can be thought of as the extended blob in an image that represents an unresolved object. In functional terms it is the spatial domain version of the optical transfer function of the imaging system. It is a useful concept in Fourier optics, astronomical imaging, medical imaging, electron microscopy and other imaging techniques such as 3D microscopy and fluorescence microscopy. The degree of spreading (blurring) of the point object is a measure for the quality of an imaging system. In non-coherent imaging systems such as fluorescent microscopes, telescopes or optical microscopes, the image formation process is linear in power and described by linear system theory. This means that when two objects A and B are imaged simultaneously, the result is equal to the sum of the independently imaged objects. In other words: the imaging of A is unaffected by the imaging of B and vice versa, owing to the non-interacting property of photons. The image of a complex object can then be seen as a convolution of the true object and the PSF. However, when the detected light is coherent, image formation is linear in the complex field. Recording the intensity image then can lead to cancellations or other non-linear effects.

Martin David Kruskal was an American mathematician and physicist. He made fundamental contributions in many areas of mathematics and science, ranging from plasma physics to general relativity and from nonlinear analysis to asymptotic analysis. His single most celebrated contribution was the discovery and theory of solitons.

Social cycle theories are among the earliest social theories in sociology. Unlike the theory of social evolutionism, which views the evolution of society and human history as progressing in some new, unique direction(s), sociological cycle theory argues that events and stages of society and history generally repeat themselves in cycles. Such a theory does not necessarily imply that there cannot be any social progress. In the early theory of Sima Qian and the more recent theories of long-term ("secular") political-demographic cycles as well as in the Varnic theory of P.R. Sarkar an explicit accounting is made of social progress.
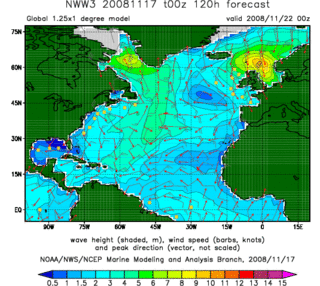
A radio propagation model, also known as the radio wave propagation model or the radio frequency propagation model, is an empirical mathematical formulation for the characterization of radio wave propagation as a function of frequency, distance and other conditions. A single model is usually developed to predict the behavior of propagation for all similar links under similar constraints. Created with the goal of formalizing the way radio waves are propagated from one place to another, such models typically predict the path loss along a link or the effective coverage area of a transmitter.
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena.
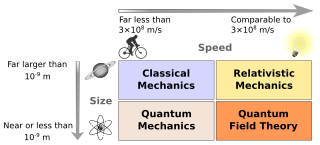
Physics deals with the combination of matter and energy. It also deals with a wide variety of systems, about which theories have been developed that are used by physicists. In general, theories are experimentally tested numerous times before they are accepted as correct as a description of Nature. For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These "central theories" are important tools for research in more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them.

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.
In quantum mechanics, a Heisenberg cut is the hypothetical interface between quantum events and an observer's information, knowledge, or conscious awareness. Below the cut everything is governed by the wave function; above the cut a classical description is used. The Heisenberg cut is a theoretical construct; it is not known whether actual Heisenberg cuts exist, where they might be found, or how they could be detected experimentally. However, the concept is useful for analysis.