
In music, just intonation or pure intonation is the tuning of musical intervals as whole number ratios of frequencies. An interval tuned in this way is said to be pure, and is called a just interval. Just intervals consist of tones from a single harmonic series of an implied fundamental. For example, in the diagram, if the notes G3 and C4 are tuned as members of the harmonic series of the lowest C, their frequencies will be 3 and 4 times the fundamental frequency. The interval ratio between C4 and G3 is therefore 4:3, a just fourth.

Pythagorean tuning is a system of musical tuning in which the frequency ratios of all intervals are based on the ratio 3:2. This ratio, also known as the "pure" perfect fifth, is chosen because it is one of the most consonant and easiest to tune by ear and because of importance attributed to the integer 3. As Novalis put it, "The musical proportions seem to me to be particularly correct natural proportions." Alternatively, it can be described as the tuning of the syntonic temperament in which the generator is the ratio 3:2, which is ≈ 702 cents wide.

Meantone temperaments are musical temperaments, that is a variety of tuning systems, obtained by narrowing the fifths so that their ratio is slightly less than 3:2, in order to push the thirds closer to pure. Meantone temperaments are constructed similarly to Pythagorean tuning, as a stack of equal fifths, but they are temperaments in that the fifths are not pure.
In music theory, an interval is a difference in pitch between two sounds. An interval may be described as horizontal, linear, or melodic if it refers to successively sounding tones, such as two adjacent pitches in a melody, and vertical or harmonic if it pertains to simultaneously sounding tones, such as in a chord.

The chromatic scale is a set of twelve pitches used in tonal music, with notes separated by the interval of a semitone. Chromatic instruments, such as the piano, are made to produce the chromatic scale, while other instruments capable of continuously variable pitch, such as the trombone and violin, can also produce microtones, or notes between those available on a piano.
Well temperament is a type of tempered tuning described in 20th-century music theory. The term is modeled on the German word wohltemperiert. This word also appears in the title of J. S. Bach's famous composition "Das wohltemperierte Klavier", The Well-Tempered Clavier.

In music theory, the syntonic comma, also known as the chromatic diesis, the Didymean comma, the Ptolemaic comma, or the diatonic comma is a small comma type interval between two musical notes, equal to the frequency ratio 81:80 (= 1.0125). Two notes that differ by this interval would sound different from each other even to untrained ears, but would be close enough that they would be more likely interpreted as out-of-tune versions of the same note than as different notes. The comma is also referred to as a Didymean comma because it is the amount by which Didymus corrected the Pythagorean major third to a just major third.

In music theory, the wolf fifth is a particularly dissonant musical interval spanning seven semitones. Strictly, the term refers to an interval produced by a specific tuning system, widely used in the sixteenth and seventeenth centuries: the quarter-comma meantone temperament. More broadly, it is also used to refer to similar intervals produced by other tuning systems, including Pythagorean and most meantone temperaments.
In musical tuning, the Pythagorean comma (or ditonic comma), named after the ancient mathematician and philosopher Pythagoras, is the small interval (or comma) existing in Pythagorean tuning between two enharmonically equivalent notes such as C and B♯, or D♭ and C♯. It is equal to the frequency ratio (1.5)12⁄27 = 531441⁄524288 ≈ 1.01364, or about 23.46 cents, roughly a quarter of a semitone (in between 75:74 and 74:73). The comma that musical temperaments often "temper" is the Pythagorean comma.

A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale, visually seen on a keyboard as the distance between two keys that are adjacent to each other. For example, C is adjacent to C♯; the interval between them is a semitone.
A schismatic temperament is a musical tuning system that results from tempering the schisma of 32805:32768 to a unison. It is also called the schismic temperament, Helmholtz temperament, or quasi-Pythagorean temperament.

In music theory, a comma is a very small interval, the difference resulting from tuning one note two different ways. Strictly speaking, there are only two kinds of comma, the syntonic comma, "the difference between a just major 3rd and four just perfect 5ths less two octaves", and the Pythagorean comma, "the difference between twelve 5ths and seven octaves". The word comma used without qualification refers to the syntonic comma, which can be defined, for instance, as the difference between an F♯ tuned using the D-based Pythagorean tuning system, and another F♯ tuned using the D-based quarter-comma meantone tuning system. Intervals separated by the ratio 81:80 are considered the same note because the 12-note Western chromatic scale does not distinguish Pythagorean intervals from 5-limit intervals in its notation. Other intervals are considered commas because of the enharmonic equivalences of a tuning system. For example, in 53TET, B♭ and A♯ are both approximated by the same interval although they are a septimal kleisma apart.
Quarter-comma meantone, or 1⁄4-comma meantone, was the most common meantone temperament in the sixteenth and seventeenth centuries, and was sometimes used later. In this system the perfect fifth is flattened by one quarter of a syntonic comma (81 : 80), with respect to its just intonation used in Pythagorean tuning ; the result is 3/2 × 1⁄4 = 4√5 ≈ 1.49535, or a fifth of 696.578 cents. This fifth is then iterated to generate the diatonic scale and other notes of the temperament. The purpose is to obtain justly intoned major thirds. It was described by Pietro Aron in his Toscanello de la Musica of 1523, by saying the major thirds should be tuned to be "sonorous and just, as united as possible." Later theorists Gioseffo Zarlino and Francisco de Salinas described the tuning with mathematical exactitude.

In music, 53 equal temperament, called 53 TET, 53 EDO, or 53 ET, is the tempered scale derived by dividing the octave into 53 equal steps. Each step represents a frequency ratio of 21⁄53, or 22.6415 cents, an interval sometimes called the Holdrian comma.
In music, 22 equal temperament, called 22-TET, 22-EDO, or 22-ET, is the tempered scale derived by dividing the octave into 22 equal steps. Each step represents a frequency ratio of 22√2, or 54.55 cents.
Kirnberger temperament is an irregular temperament developed in the second half of the 18th century by Johann Kirnberger. Kirnberger was a student of Johann Sebastian Bach, held great admiration for his teacher and was one of his principal proponents.
Werckmeister temperaments are the tuning systems described by Andreas Werckmeister in his writings. The tuning systems are numbered in two different ways: the first refers to the order in which they were presented as "good temperaments" in Werckmeister's 1691 treatise, the second to their labelling on his monochord. The monochord labels start from III since just intonation is labelled I and quarter-comma meantone is labelled II. The temperament commonly known as "Werckmeister III" is referred to in this article as "Werckmeister I (III)".
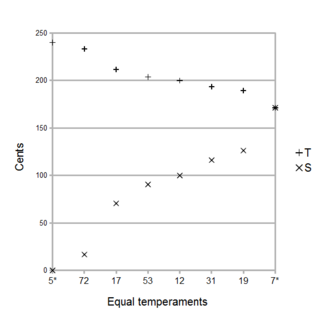
A regular diatonic tuning is any musical scale consisting of "tones" (T) and "semitones" (S) arranged in any rotation of the sequence TTSTTTS which adds up to the octave with all the T's being the same size and all the S's the being the same size, with the 'S's being smaller than the 'T's. In such a tuning, then the notes are connected together in a chain of seven fifths, all the same size which makes it a Linear temperament with the tempered fifth as a generator.

Five-limit tuning, 5-limit tuning, or 5-prime-limit tuning (not to be confused with 5-odd-limit tuning), is any system for tuning a musical instrument that obtains the frequency of each note by multiplying the frequency of a given reference note (the base note) by products of integer powers of 2, 3, or 5 (prime numbers limited to 5 or lower), such as 2−3·31·51 = 15/8.
The circulating temperament today referred to as Vallotti temperament is a shifted version of Young's second temperament. Its attribution to the 18th-century organist, composer, and music theorist, Francesco Vallotti is a mistake, since there is no evidence that he ever suggested it. It is however audibly indistinguishable from a slightly different temperament that was in fact devised by Vallotti.










