Electrical resistivity is a fundamental property of a material that quantifies how strongly that material opposes the flow of electric current. A low resistivity indicates a material that readily allows the flow of electric current. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-metre (Ω⋅m). As an example, if a 1 m × 1 m × 1 m solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is 1 Ω, then the resistivity of the material is 1 Ω⋅m.

In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of continuum mechanics. The fundamental "linearizing" assumptions of linear elasticity are: infinitesimal strains or "small" deformations and linear relationships between the components of stress and strain. In addition linear elasticity is valid only for stress states that do not produce yielding. These assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis.

The Einstein–Hilbert action in general relativity is the action that yields the Einstein field equations through the principle of least action. With the (− + + +) metric signature, the gravitational part of the action is given as
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.
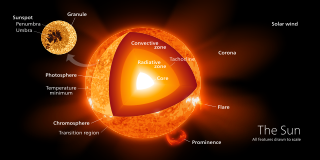
A radiation zone, or radiative region is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiation zone in the form of electromagnetic radiation as photons.

Collision theory is a theory that was proposed independently by Max Trautz in 1916 and William Lewis in 1918, that qualitatively explains how chemical reactions occur and why reaction rates differ for different reactions. The collision theory states that when suitable particles of the reactant hit each other, only a certain fraction of the collisions cause any noticeable or significant chemical change; these successful changes are called successful collisions. The successful collisions must have enough energy, also known as activation energy, at the moment of impact to break the preexisting bonds and form all new bonds. This results in the products of the reaction. Increasing the concentration of the reactant particles or raising the temperature - which brings about more collisions and hence more successful collisions - therefore increases the rate of a reaction.

The mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.
The nuclear cross section of a nucleus is used to characterize the probability that a nuclear reaction will occur. The concept of a nuclear cross section can be quantified physically in terms of "characteristic area" where a larger area means a larger probability of interaction. The standard unit for measuring a nuclear cross section is the barn, which is equal to 10−28 m² or 10−24 cm². Cross sections can be measured for all possible interaction processes together, in which case they are called total cross sections, or for specific processes, distinguishing elastic scattering and inelastic scattering; of the latter, amongst neutron cross sections the absorption cross sections are of particular interest.
Aeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows. A notable example of this phenomenon is the Aeolian tones produced by wind blowing over fixed objects.
Lattice Boltzmann methods (LBM) is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations, the discrete Boltzmann equation is solved to simulate the flow of a Newtonian fluid with collision models such as Bhatnagar–Gross–Krook (BGK). By simulating streaming and collision processes across a limited number of particles, the intrinsic particle interactions evince a microcosm of viscous flow behavior applicable across the greater mass.

The Lorenz system is a system of ordinary differential equations first studied by Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system which, when plotted, resemble a butterfly or figure eight.
Material selection is a step in the process of designing any physical object. In the context of product design, the main goal of material selection is to minimize cost while meeting product performance goals. Systematic selection of the best material for a given application begins with properties and costs of candidate materials. For example, a thermal blanket must have poor thermal conductivity in order to minimize heat transfer for a given temperature difference.
In mathematics — specifically, in stochastic analysis — an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
The Taft equation is a linear free energy relationship (LFER) used in physical organic chemistry in the study of reaction mechanisms and in the development of quantitative structure activity relationships for organic compounds. It was developed by Robert W. Taft in 1952 as a modification to the Hammett equation. While the Hammett equation accounts for how field, inductive, and resonance effects influence reaction rates, the Taft equation also describes the steric effects of a substituent. The Taft equation is written as:
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum. In convective form it is written:
In physical organic chemistry, the Grunwald–Winstein equation is a linear free energy relationship between relative rate constants and the ionizing power of various solvent systems, describing the effect of solvent as nucleophile on different substrates. The equation, which was developed by Ernest Grunwald and Saul Winstein in 1948, could be written
In physical organic chemistry, the Swain-Lupton equation is a linear free energy relationship (LFER) that is used in the study of reaction mechanisms and in the development of quantitative structure activity relationships for organic compounds. It was developed by C. Gardner Swain and Elmer C. Lupton Jr. in 1968 as a refinement of the Hammett equation to include both field effects and resonance effects.















