In mathematics, the associative property is a property of some binary operations. In propositional logic, associativity is a valid rule of replacement for expressions in logical proofs.
An allele is a variant form of a given gene, meaning it is one of two or more versions of a known mutation at the same place on a chromosome. It can also refer to different sequence variations for a several-hundred base-pair or more region of the genome that codes for a protein. Alleles can come in different extremes of size. At the lowest possible end one can be the single base choice of an SNP. At the higher end, it can be the sequence variations for the regions of the genome that code for the same protein which can be up to several thousand base-pairs long.
RSA (Rivest–Shamir–Adleman) is one of the first public-key cryptosystems and is widely used for secure data transmission. In such a cryptosystem, the encryption key is public and it is different from the decryption key which is kept secret (private). In RSA, this asymmetry is based on the practical difficulty of the factorization of the product of two large prime numbers, the "factoring problem". The acronym RSA is made of the initial letters of the surnames of Ron Rivest, Adi Shamir, and Leonard Adleman, who first publicly described the algorithm in 1977. Clifford Cocks, an English mathematician working for the British intelligence agency Government Communications Headquarters (GCHQ), had developed an equivalent system in 1973, but this was not declassified until 1997.

In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.
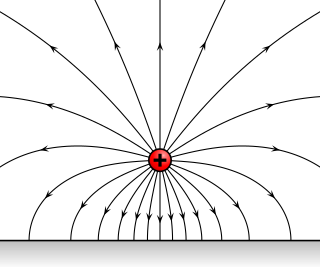
An electric field surrounds an electric charge, and exerts force on other charges in the field, attracting or repelling them. Electric field is sometimes abbreviated as E-field. The electric field is defined mathematically as a vector field that associates to each point in space the force per unit of charge exerted on an infinitesimal positive test charge at rest at that point. The SI unit for electric field strength is volt per meter (V/m). Newtons per coulomb (N/C) is also used as a unit of electric field strength. Electric fields are created by electric charges, or by time-varying magnetic fields. Electric fields are important in many areas of physics, and are exploited practically in electrical technology. On an atomic scale, the electric field is responsible for the attractive force between the atomic nucleus and electrons that holds atoms together, and the forces between atoms that cause chemical bonding. Electric fields and magnetic fields are both manifestations of the electromagnetic force, one of the four fundamental forces of nature.

Division is one of the four basic operations of arithmetic, the ways that numbers are combined to make new numbers. The other operations are addition, subtraction, and multiplication. Several symbols are used for the division operator, including the obelus (÷), the colon (:) and the slash (/).

Exclusive or or exclusive disjunction is a logical operation that outputs true only when inputs differ.

Capacitance is the ratio of the change in an electric charge in a system to the corresponding change in its electric potential. There are two closely related notions of capacitance: self capacitance and mutual capacitance. Any object that can be electrically charged exhibits self capacitance. A material with a large self capacitance holds more electric charge at a given voltage than one with low capacitance. The notion of mutual capacitance is particularly important for understanding the operations of the capacitor, one of the three elementary linear electronic components.
Hamiltonian mechanics is a theory developed as a reformulation of classical mechanics and predicts the same outcomes as non-Hamiltonian classical mechanics. It uses a different mathematical formalism, providing a more abstract understanding of the theory. Historically, it was an important reformulation of classical mechanics, which later contributed to the formulation of statistical mechanics and quantum mechanics.

In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Most familiar as the name of the property that says "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it ; such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized. A corresponding property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.

Quantitative genetics is a branch of population genetics that deals with phenotypes that vary continuously —as opposed to discretely identifiable phenotypes and gene-products.
A conventional marginal cost is incremented by one unit; that is, it is the cost of producing one more unit of a good. Intuitively, marginal cost at each level of production includes the cost of any additional inputs required to produce the next unit. At each level of production and time period being considered, marginal costs include all costs that vary with the level of production, whereas other costs that do not vary with production are fixed and thus have no marginal cost. For example, the marginal cost of producing an automobile will generally include the costs of labor and parts needed for the additional automobile but not the fixed costs of the factory that have already been incurred. In practice, marginal analysis is segregated into short and long-run cases, so that, over the long run, all costs become marginal. Where there are economies of scale, prices set at marginal cost will fail to cover total costs, thus requiring a subsidy. Marginal cost pricing is not a matter of merely lowering the general level of prices with the aid of a subsidy; with or without subsidy it calls for a drastic restructuring of pricing practices, with opportunities for very substantial improvements in efficiency at critical points.

The De Havilland Canada DHC-8, commonly known as the Dash 8, is a series of turboprop-powered regional airliners, introduced by de Havilland Canada (DHC) in 1984. DHC was later bought by Boeing in 1988, then by Bombardier in 1992; then by Longview Aviation Capital in 2019, reviving the de Havilland Canada brand. Powered by two Pratt & Whitney Canada PW100s, it was developed from the Dash 7 with improved cruise performance, lowered operational costs but without STOL performance. Three sizes were offered: initially the 37–40 seat -100 until 2005 and the more powerful -200 from 1995, the stretched 50–56 seats -300 from 1989, both until 2009, and the 68–90 seats -400 from 1999, still in production. The Q Series are post-1997 variants fitted with active noise control systems.

In motorsport the pole position is the position at the inside of the front row at the start of a racing event. This position is typically given to the vehicle and driver with the best qualifying time in the trials before the race. This number-one qualifying driver is referred to as the pole sitter.

In computing, the modulo operation finds the remainder after division of one number by another.

A capacitor is a device that stores electrical energy in an electric field. It is a passive electronic component with two terminals.
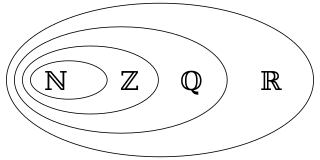
In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q ; it was thus denoted in 1895 by Giuseppe Peano after quoziente, Italian for "quotient".
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid.

Coulomb's law, or Coulomb's inverse-square law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is conventionally called electrostatic force or Coulomb force. The quantity of electrostatic force between stationary charges is always described by Coulomb's law. The law was first published in 1785 by French physicist Charles-Augustin de Coulomb, and was essential to the development of the theory of electromagnetism, maybe even its starting point, because it was now possible to discuss quantity of electric charge in a meaningful way.












