This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
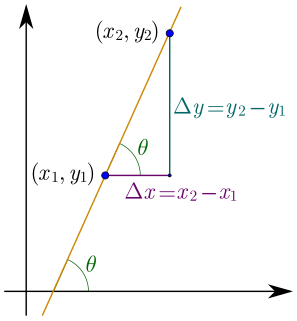
In mathematics, the slope or gradient of a line is a number that describes both the direction and the steepness of the line. Slope is often denoted by the letter m; there is no clear answer to the question why the letter m is used for slope, but it might be from the "m for multiple" in the equation of a straight line "y = mx + b" or "y = mx + c".

In photography, angle of view (AOV) describes the angular extent of a given scene that is imaged by a camera. It is used interchangeably with the more general term field of view.

The angular aperture of a lens is the angular size of the lens aperture as seen from the focal point:

The Gudermannian function, named after Christoph Gudermann (1798–1852), relates the circular functions and hyperbolic functions without explicitly using complex numbers.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

In mathematics, trigonometric substitution is the substitution of trigonometric functions for other expressions. One may use the trigonometric identities to simplify certain integrals containing radical expressions:
Substitution 1. If the integrand contains a2 − x2, let
and use the identity
Substitution 2. If the integrand contains a2 + x2, let
and use the identity
Substitution 3. If the integrand contains x2 − a2, let
and use the identity

The great-circle distance or orthodromic distance is the shortest distance between two points on the surface of a sphere, measured along the surface of the sphere. The distance between two points in Euclidean space is the length of a straight line between them, but on the sphere there are no straight lines. In spaces with curvature, straight lines are replaced by geodesics. Geodesics on the sphere are circles on the sphere whose centers coincide with the center of the sphere, and are called great circles.
In mathematics, a quadratic integral is an integral of the form
In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet.
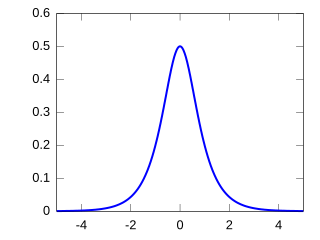
In probability theory and statistics, the hyperbolic secant distribution is a continuous probability distribution whose probability density function and characteristic function are proportional to the hyperbolic secant function. The hyperbolic secant function is equivalent to the reciprocal hyperbolic cosine, and thus this distribution is also called the inverse-cosh distribution.
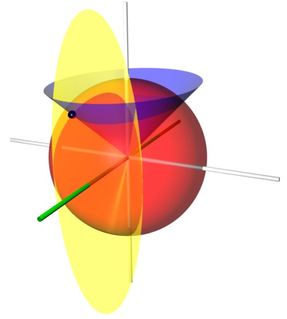
Conical coordinates are a three-dimensional orthogonal coordinate system consisting of
concentric spheres and by two families of perpendicular cones, aligned along the z- and x-axes, respectively.
The n-vector representation is a three-parameter non-singular representation well-suited for replacing latitude and longitude as horizontal position representation in mathematical calculations and computer algorithms.

The Hammer projection is an equal-area map projection described by Ernst Hammer in 1892. Using the same 2:1 elliptical outer shape as the Mollweide projection, Hammer intended to reduce distortion in the regions of the outer meridians, where it is extreme in the Mollweide.
This is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus.
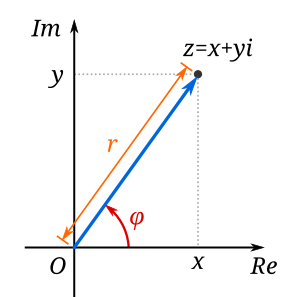
In mathematics, the argument is a multi-valued function operating on the nonzero complex numbers. With complex number z visualized as a point in the complex plane, the argument of z is the angle between the positive real axis and the line joining the point to the origin, shown as φ in figure 1 and denoted arg z. To define a single-valued function, the principal value of the argument is used. It is chosen to be the unique value of the argument that lies within the interval (–π, π].

The Gall stereographic projection, presented by James Gall in 1855, is a cylindrical projection. It is neither equal-area nor conformal but instead tries to balance the distortion inherent in any projection.













