The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. This includes polynomials with real coefficients, since every real number can be considered a complex number with its imaginary part equal to zero.
In probability theory, Chebyshev's inequality guarantees that, for a wide class of probability distributions, no more than a certain fraction of values can be more than a certain distance from the mean. Specifically, no more than 1/k2 of the distribution's values can be more than k standard deviations away from the mean. The rule is often called Chebyshev's theorem, about the range of standard deviations around the mean, in statistics. The inequality has great utility because it can be applied to any probability distribution in which the mean and variance are defined. For example, it can be used to prove the weak law of large numbers.

In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree over a set of equispaced interpolation points. It was discovered by Carl David Tolmé Runge (1901) when exploring the behavior of errors when using polynomial interpolation to approximate certain functions. The discovery was important because it shows that going to higher degrees does not always improve accuracy. The phenomenon is similar to the Gibbs phenomenon in Fourier series approximations.
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant. It is named after the Russian mathematician Andrey Markov, although it appeared earlier in the work of Pafnuty Chebyshev, and many sources, especially in analysis, refer to it as Chebyshev's inequality or Bienaymé's inequality.
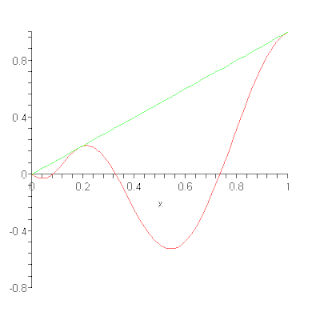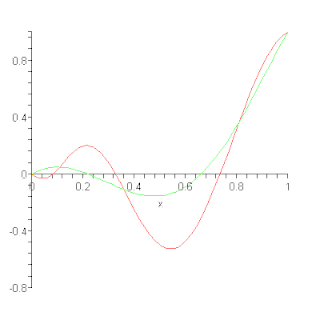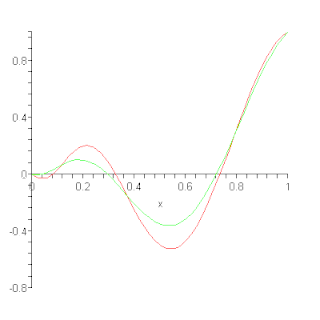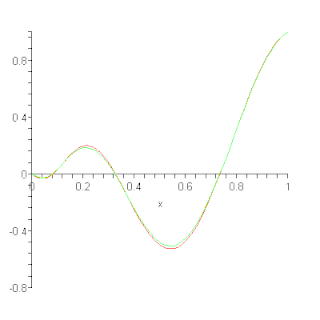
In the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials.
In probability theory, the Chernoff bound, named after Herman Chernoff but due to Herman Rubin, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is a sharper bound than the known first- or second-moment-based tail bounds such as Markov's inequality or Chebyshev's inequality, which only yield power-law bounds on tail decay. However, the Chernoff bound requires that the variates be independent – a condition that neither Markov's inequality nor Chebyshev's inequality require, although Chebyshev's inequality does require the variates to be pairwise independent.
In probability theory, Hoeffding's inequality provides an upper bound on the probability that the sum of bounded independent random variables deviates from its expected value by more than a certain amount. Hoeffding's inequality was proven by Wassily Hoeffding in 1963.
In mathematics, the Lebesgue constants give an idea of how good the interpolant of a function is in comparison with the best polynomial approximation of the function. The Lebesgue constant for polynomials of degree at most n and for the set of n + 1 nodes T is generally denoted by Λn(T ). These constants are named after Henri Lebesgue.
In mathematics, the Landau–Kolmogorov inequality, named after Edmund Landau and Andrey Kolmogorov, is the following family of interpolation inequalities between different derivatives of a function f defined on a subset T of the real numbers:
In probability theory, Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive ,
In mathematics, a univariate polynomial of degree n with real or complex coefficients has n complex roots, if counted with their multiplicities. They form a set of n points in the complex plane. This article concerns the geometry of these points, that is the information about their localization in the complex plane that can be deduced from the degree and the coefficients of the polynomial.
In mathematical analysis, the Chebyshev–Markov–Stieltjes inequalities are inequalities related to the problem of moments that were formulated in the 1880s by Pafnuty Chebyshev and proved independently by Andrey Markov and by Thomas Jan Stieltjes. Informally, they provide sharp bounds on a measure from above and from below in terms of its first moments.
In approximation theory, Jackson's inequality is an inequality bounding the value of function's best approximation by algebraic or trigonometric polynomials in terms of the modulus of continuity or modulus of smoothness of the function or of its derivatives. Informally speaking, the smoother the function is, the better it can be approximated by polynomials.
In mathematics, particularly numerical analysis, the Bramble–Hilbert lemma, named after James H. Bramble and Stephen Hilbert, bounds the error of an approximation of a function by a polynomial of order at most in terms of derivatives of of order . Both the error of the approximation and the derivatives of are measured by norms on a bounded domain in . This is similar to classical numerical analysis, where, for example, the error of linear interpolation can be bounded using the second derivative of . However, the Bramble–Hilbert lemma applies in any number of dimensions, not just one dimension, and the approximation error and the derivatives of are measured by more general norms involving averages, not just the maximum norm.
In mathematics, Welch bounds are a family of inequalities pertinent to the problem of evenly spreading a set of unit vectors in a vector space. The bounds are important tools in the design and analysis of certain methods in telecommunication engineering, particularly in coding theory. The bounds were originally published in a 1974 paper by L. R. Welch.
In probability theory, concentration inequalities provide bounds on how a random variable deviates from some value. The law of large numbers of classical probability theory states that sums of independent random variables are, under very mild conditions, close to their expectation with a large probability. Such sums are the most basic examples of random variables concentrated around their mean. Recent results show that such behavior is shared by other functions of independent random variables.
Quantum refereed game in quantum information processing is a class of games in the general theory of quantum games. It is played between two players, Alice and Bob, and arbitrated by a referee. The referee outputs the pay-off for the players after interacting with them for a fixed number of rounds, while exchanging quantum information.





