In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
In graph theory, a branch of mathematics and computer science, the Chinese postman problem (CPP), postman tour or route inspection problem is to find a shortest closed path or circuit that visits every edge of an (connected) undirected graph. When the graph has an Eulerian circuit, that circuit is an optimal solution. Otherwise, the optimization problem is to find the smallest number of graph edges to duplicate so that the resulting multigraph does have an Eulerian circuit. It may be solved in polynomial time.

The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1736 laid the foundations of graph theory and prefigured the idea of topology.
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a Hamiltonian path that is a cycle. Determining whether such paths and cycles exist in graphs is the Hamiltonian path problem, which is NP-complete.
In graph theory, a branch of mathematics, the (binary) cycle space of an undirected graph is the set of its Eulerian subgraphs.
This is a glossary of graph theory terms. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by edges.

In graph theory, an Eulerian trail is a trail in a finite graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is an Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. The problem can be stated mathematically like this:
In the mathematical discipline of graph theory, Menger's theorem says that in a finite graph, the size of a minimum cut set is equal to the maximum number of disjoint paths that can be found between any pair of vertices. Proved by Karl Menger in 1927, it characterizes the connectivity of a graph. It is generalized by the max-flow min-cut theorem, which is a weighted, edge version, and which in turn is a special case of the strong duality theorem for linear programs.

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, and in a multigraph, loops are counted twice. The degree of a vertex is denoted or . The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the multigraph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, all degrees are the same, and so we can speak of the degree of the graph. A complete graph is a special kind of regular graph where all vertices,p ,have the maximum degree, p-1. A complete graph is denoted with the form Kp where p is the number of vertices in the graph.
In mathematics, a universal graph is an infinite graph that contains every finite graph as an induced subgraph. A universal graph of this type was first constructed by Richard Rado and is now called the Rado graph or random graph. More recent work has focused on universal graphs for a graph family F: that is, an infinite graph belonging to F that contains all finite graphs in F. For instance, the Henson graphs are universal in this sense for the i-clique-free graphs.
In graph theory, a part of discrete mathematics, the BEST theorem gives a product formula for the number of Eulerian circuits in directed (oriented) graphs. The name is an acronym of the names of people who discovered it: de Bruijn, van Aardenne-Ehrenfest, Smith and Tutte.

In the mathematical discipline of graph theory, the dual graph of a plane graph G is a graph that has a vertex for each face of G. The dual graph has an edge whenever two faces of G are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is an edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.
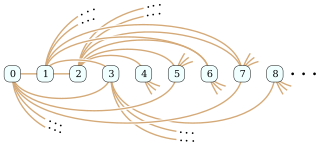
In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann (1937). The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

In graph theory, a branch of mathematics, the handshaking lemma is the statement that every finite undirected graph has an even number of vertices with odd degree. In more colloquial terms, in a party of people some of whom shake hands, an even number of people must have shaken an odd number of other people's hands.
In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős (1951), after whom it is named.
Frucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph. More strongly, for any finite group G there exist infinitely many non-isomorphic simple connected graphs such that the automorphism group of each of them is isomorphic to G.
In the mathematical discipline of graph theory, 2-factor theorem discovered by Julius Petersen, is one of the earliest works in graph theory and can be stated as follows:

Leonhard Euler was a Swiss mathematician, physicist, astronomer, logician and engineer, who made important and influential discoveries in many branches of mathematics, such as infinitesimal calculus and graph theory, while also making pioneering contributions to several branches such as topology and analytic number theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory.
Gert Sabidussi is an Austrian mathematician specializing in combinatorics and graph theory.
The Canadian Journal of Mathematics is a bimonthly mathematics journal published by the Canadian Mathematical Society.