
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
In computer science, a red–black tree is a self-balancing binary search tree data structure noted for fast storage and retrieval of ordered information. The nodes in a red-black tree hold an extra "color" bit, often drawn as red and black, which help ensure that the tree is always approximately balanced.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information".
In computing, a persistent data structure or not ephemeral data structure is a data structure that always preserves the previous version of itself when it is modified. Such data structures are effectively immutable, as their operations do not (visibly) update the structure in-place, but instead always yield a new updated structure. The term was introduced in Driscoll, Sarnak, Sleator, and Tarjan's 1986 article.
In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.
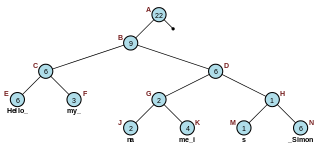
In computer programming, a rope, or cord, is a data structure composed of smaller strings that is used to efficiently store and manipulate a very long string. For example, a text editing program may use a rope to represent the text being edited, so that operations such as insertion, deletion, and random access can be done efficiently.
A B+ tree is an m-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.
In computer science, an interval tree is a tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for instance, to find all roads on a computerized map inside a rectangular viewport, or to find all visible elements inside a three-dimensional scene. A similar data structure is the segment tree.

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. K-dimensional is that which concerns exactly k orthogonal axes or a space of any number of dimensions. k-d trees are a useful data structure for several applications, such as:
In graph theory and computer science, the lowest common ancestor (LCA) of two nodes v and w in a tree or directed acyclic graph (DAG) T is the lowest node that has both v and w as descendants, where we define each node to be a descendant of itself.
A link/cut tree is a data structure for representing a forest, a set of rooted trees, and offers the following operations:
In computer science, a range tree is an ordered tree data structure to hold a list of points. It allows all points within a given range to be reported efficiently, and is typically used in two or higher dimensions. Range trees were introduced by Jon Louis Bentley in 1979. Similar data structures were discovered independently by Lueker, Lee and Wong, and Willard. The range tree is an alternative to the k-d tree. Compared to k-d trees, range trees offer faster query times of but worse storage of , where n is the number of points stored in the tree, d is the dimension of each point and k is the number of points reported by a given query.

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
In computational geometry, the Bentley–Ottmann algorithm is a sweep line algorithm for listing all crossings in a set of line segments, i.e. it finds the intersection points of line segments. It extends the Shamos–Hoey algorithm, a similar previous algorithm for testing whether or not a set of line segments has any crossings. For an input consisting of line segments with crossings, the Bentley–Ottmann algorithm takes time . In cases where , this is an improvement on a naïve algorithm that tests every pair of segments, which takes .

A Fenwick tree or binary indexed tree(BIT) is a data structure that can efficiently update values and calculate prefix sums in an array of values.
In computer science, a double-ended priority queue (DEPQ) or double-ended heap is a data structure similar to a priority queue or heap, but allows for efficient removal of both the maximum and minimum, according to some ordering on the keys (items) stored in the structure. Every element in a DEPQ has a priority or value. In a DEPQ, it is possible to remove the elements in both ascending as well as descending order.
In computer science, an x-fast trie is a data structure for storing integers from a bounded domain. It supports exact and predecessor or successor queries in time O(log log M), using O(n log M) space, where n is the number of stored values and M is the maximum value in the domain. The structure was proposed by Dan Willard in 1982, along with the more complicated y-fast trie, as a way to improve the space usage of van Emde Boas trees, while retaining the O(log log M) query time.
In computer science, the range query problem consists of efficiently answering several queries regarding a given interval of elements within an array. For example, a common task, known as range minimum query, is finding the smallest value inside a given range within a list of numbers.

In computer science, a finger search on a data structure is an extension of any search operation that structure supports, where a reference (finger) to an element in the data structure is given along with the query. While the search time for an element is most frequently expressed as a function of the number of elements in a data structure, finger search times are a function of the distance between the element and the finger.









