In geometry, a bicone or dicone (from Latin : bi-, and Greek: di-, both meaning "two") is the three-dimensional surface of revolution of a rhombus around one of its axes of symmetry. Equivalently, a bicone is the surface created by joining two congruent, right, circular cones at their bases.
A bicone has circular symmetry and orthogonal bilateral symmetry.
For a circular bicone with radius R and height center-to-top H, the formula for volume becomes
For a right circular cone, the surface area is
| Bipyramid name | Digonal bipyramid | Triangular bipyramid (See: J12) | Square bipyramid (See: O) | Pentagonal bipyramid (See: J13) | Hexagonal bipyramid | Heptagonal bipyramid | Octagonal bipyramid | Enneagonal bipyramid | Decagonal bipyramid | ... | Apeirogonal bipyramid |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image |  |  |  |  |  |  |  |  | ... | ||
| Spherical tiling image |  |  |  |  |  |  |  |  |  | Plane tiling image |  |
| Face config. | V2.4.4 | V3.4.4 | V4.4.4 | V5.4.4 | V6.4.4 | V7.4.4 | V8.4.4 | V9.4.4 | V10.4.4 | ... | V∞.4.4 |
| Coxeter diagram |     |  |  |  |  |  |  |  |  | ... |  |
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid.
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
The steradian or square radian is the unit of solid angle in the International System of Units (SI). It is used in three-dimensional geometry, and is analogous to the radian, which quantifies planar angles. Whereas an angle in radians, projected onto a circle, gives a length on the circumference, a solid angle in steradians, projected onto a sphere, gives an area on the surface. The name is derived from the Greek στερεός stereos 'solid' + radian.
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are polygonal, the side faces are trapezoidal. A right frustum is a right pyramid or a right cone truncated perpendicularly to its axis; otherwise it is an oblique frustum.
In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.
In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.
In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a "diamond", after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.
The Method of Mechanical Theorems, also referred to as The Method, is one of the major surviving works of the ancient Greek polymath Archimedes. The Method takes the form of a letter from Archimedes to Eratosthenes, the chief librarian at the Library of Alexandria, and contains the first attested explicit use of indivisibles. The work was originally thought to be lost, but in 1906 was rediscovered in the celebrated Archimedes Palimpsest. The palimpsest includes Archimedes' account of the "mechanical method", so called because it relies on the center of weights of figures (centroid) and the law of the lever, which were demonstrated by Archimedes in On the Equilibrium of Planes.
In solid geometry, the sphericon is a solid that has a continuous developable surface with two congruent, semi-circular edges, and four vertices that define a square. It is a member of a special family of rollers that, while being rolled on a flat surface, bring all the points of their surface to contact with the surface they are rolling on. It was discovered independently by carpenter Colin Roberts in the UK in 1969, by dancer and sculptor Alan Boeding of MOMIX in 1979, and by inventor David Hirsch, who patented it in Israel in 1980.
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.
A cylinder has traditionally been a three-dimensional solid, one of the most basic of curvilinear geometric shapes. In elementary geometry, it is considered a prism with a circle as its base.
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere.
In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by these axes, is sometimes referred to as a contour line; for example, if a plane cuts through mountains of a raised-relief map parallel to the ground, the result is a contour line in two-dimensional space showing points on the surface of the mountains of equal elevation.
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body. This theorem has particular application to astronomy.
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a lateral face. It is a conic solid with polygonal base. A pyramid with an n-sided base has n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.
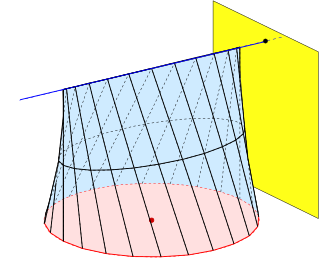
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions:
In geometry, a hypercone is the figure in the 4-dimensional Euclidean space represented by the equation
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:
In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle.
In geometry, a polycon is a kind of a developable roller. It is made of identical pieces of a cone whose apex angle equals the angle of an even sided regular polygon. In principle, there are infinitely many polycons, as many as there are even sided regular polygons. Most members of the family have elongated spindle like shapes. The polycon family generalizes the sphericon. It was discovered by the Israeli inventor David Hirsch in 2017
 | This elementary geometry-related article is a stub. You can help Wikipedia by expanding it. |
