Boy's surface

Last updated June 22, 2023

In geometry, Boy's surface is an immersion of the real projective plane in 3-dimensional space found by Werner Boy in 1901. He discovered it on assignment from David Hilbert to prove that the projective plane could not be immersed in 3-space.

Parametrization

Boy's surface can be parametrized in several ways. One parametrization, discovered by Rob Kusner and Robert Bryant,^[4] is the following: given a complex number w whose magnitude is less than or equal to one ( $\|w\|\leq 1$ ), let

{\begin{aligned}g_{1}&=-{3 \over 2}\operatorname {Im} \left[{w\left(1-w^{4}\right) \over w^{6}+{\sqrt {5}}w^{3}-1}\right]\\[4pt]g_{2}&=-{3 \over 2}\operatorname {Re} \left[{w\left(1+w^{4}\right) \over w^{6}+{\sqrt {5}}w^{3}-1}\right]\\[4pt]g_{3}&=\operatorname {Im} \left[{1+w^{6} \over w^{6}+{\sqrt {5}}w^{3}-1}\right]-{1 \over 2}\\\end{aligned}}

and then set

{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\frac {1}{g_{1}^{2}+g_{2}^{2}+g_{3}^{2}}}{\begin{pmatrix}g_{1}\\g_{2}\\g_{3}\end{pmatrix}}

we then obtain the Cartesian coordinates x, y, and z of a point on the Boy's surface.

If one performs an inversion of this parametrization centered on the triple point, one obtains a complete minimal surface with three ends (that's how this parametrization was discovered naturally). This implies that the Bryant–Kusner parametrization of Boy's surfaces is "optimal" in the sense that it is the "least bent" immersion of a projective plane into three-space.

Property of Bryant–Kusner parametrization

If w is replaced by the negative reciprocal of its complex conjugate, ${\textstyle -{1 \over w^{\star }},}$ then the functions g₁, g₂, and g₃ of w are left unchanged.

By replacing $w$ in terms of its real and imaginary parts $w = s + it$ , and expanding resulting parameterization, one may obtain a parameterization of Boy's surface in terms of rational functions of $s$ and $t$ . This shows that Boy's surface is not only an algebraic surface, but even a rational surface. The remark of the preceding paragraph shows that the generic fiber of this parameterization consists of two points (that is that almost every point of Boy's surface may be obtained by two parameters values).

Relation to the real projective plane

Let $P(w)=(x(w),y(w),z(w))$ be the Bryant–Kusner parametrization of Boy's surface. Then

P(w)=P\left(-{1 \over w^{\star }}\right).

This explains the condition $\left\|w\right\|\leq 1$ on the parameter: if $\left\|w\right\|<1,$ then ${\textstyle \left\|-{1 \over w^{\star }}\right\|>1.}$ However, things are slightly more complicated for $\left\|w\right\|=1.$ In this case, one has ${\textstyle -{1 \over w^{\star }}=-w.}$ This means that, if $\left\|w\right\|=1,$ the point of the Boy's surface is obtained from two parameter values: $P(w)=P(-w).$ In other words, the Boy's surface has been parametrized by a disk such that pairs of diametrically opposite points on the perimeter of the disk are equivalent. This shows that the Boy's surface is the image of the real projective plane, RP² by a smooth map. That is, the parametrization of the Boy's surface is an immersion of the real projective plane into the Euclidean space.

Symmetries

Boy's surface has 3-fold symmetry. This means that it has an axis of discrete rotational symmetry: any 120° turn about this axis will leave the surface looking exactly the same. The Boy's surface can be cut into three mutually congruent pieces.

Applications

Boy's surface can be used in sphere eversion, as a half-way model. A half-way model is an immersion of the sphere with the property that a rotation interchanges inside and outside, and so can be employed to evert (turn inside-out) a sphere. Boy's (the case p = 3) and Morin's (the case p = 2) surfaces begin a sequence of half-way models with higher symmetry first proposed by George Francis, indexed by the even integers 2p (for p odd, these immersions can be factored through a projective plane). Kusner's parametrization yields all these.

Model at Oberwolfach

Model of a Boy's surface in Oberwolfach Boyflaeche.JPG — Model of a Boy's surface in Oberwolfach

The Mathematical Research Institute of Oberwolfach has a large model of a Boy's surface outside the entrance, constructed and donated by Mercedes-Benz in January 1991. This model has 3-fold rotational symmetry and minimizes the Willmore energy of the surface. It consists of steel strips which represent the image of a polar coordinate grid under a parameterization given by Robert Bryant and Rob Kusner. The meridians (rays) become ordinary Möbius strips, i.e. twisted by 180 degrees. All but one of the strips corresponding to circles of latitude (radial circles around the origin) are untwisted, while the one corresponding to the boundary of the unit circle is a Möbius strip twisted by three times 180 degrees — as is the emblem of the institute ( Mathematisches Forschungsinstitut Oberwolfach 2011 ).

Model made for Clifford Stoll

A model was made in glass by glassblower Lucas Clarke, with the cooperation of Adam Savage, for presentation to Clifford Stoll, It was featured on Adam Savage's YouTube channel, Tested. All three appeared in the video discussing it.^[5]

Related Research Articles

In mathematics, the Klein bottle is an example of a non-orientable surface; that is, informally, a one-sided surface which, if traveled upon, could be followed back to the point of origin while flipping the traveler upside down. More formally, the Klein bottle is a two-dimensional manifold on which one cannot define a normal vector at each point that varies continuously over the whole manifold. Other related non-orientable surfaces include the Möbius strip and the real projective plane. While a Möbius strip is a surface with boundary, a Klein bottle has no boundary. For comparison, a sphere is an orientable surface with no boundary.

In geometry, a pseudosphere is a surface with constant negative Gaussian curvature.

<span class="mw-page-title-main">Curvature</span> Mathematical measure of how much a curve or surface deviates from flatness

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.

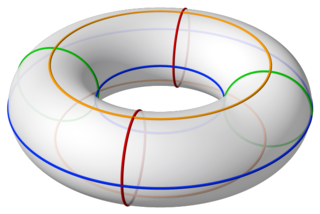
In geometry, a torus is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanar with the circle. The main types of toruses include ring toruses, horn toruses, and spindle toruses. A ring torus is sometimes colloquially referred to as a donut or doughnut.

In mathematics, conformal geometry is the study of the set of angle-preserving (conformal) transformations on a space.

In mathematics and physics, n-dimensional anti-de Sitter space (AdS_n) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire $(n - 1)$ -dimensional flat of fixed points in a $n$ -dimensional space.

In mathematics, and more specifically in geometry, parametrization is the process of finding parametric equations of a curve, a surface, or, more generally, a manifold or a variety, defined by an implicit equation. The inverse process is called implicitization. "To parameterize" by itself means "to express in terms of parameters".

In mathematics, the mean curvature $of a surface is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space.$

In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.

In geometry, a three-dimensional space is a mathematical space in which three values (coordinates) are required to determine the position of a point. Most commonly, it is the three-dimensional Euclidean space, the Euclidean n-space of dimension n=3 that models physical space. More general three-dimensional spaces are called 3-manifolds.

A parametric surface is a surface in the Euclidean space $which is defined by a parametric equation with two parameters :\mathbb {R} ^{2}\to \mathbb {R} ^{3}} . Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.$

In mathematics, an immersion is a differentiable function between differentiable manifolds whose differential pushforward is everywhere injective. Explicitly, $f : M \to N$ is an immersion if

<span class="mw-page-title-main">Scherk surface</span>

In mathematics, a Scherk surface is an example of a minimal surface. Scherk described two complete embedded minimal surfaces in 1834; his first surface is a doubly periodic surface, his second surface is singly periodic. They were the third non-trivial examples of minimal surfaces. The two surfaces are conjugates of each other.

In geometry, minimax eversions are a class of sphere eversions, constructed by using half-way models.

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric. Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

A gyrovector space is a mathematical concept proposed by Abraham A. Ungar for studying hyperbolic geometry in analogy to the way vector spaces are used in Euclidean geometry. Ungar introduced the concept of gyrovectors that have addition based on gyrogroups instead of vectors which have addition based on groups. Ungar developed his concept as a tool for the formulation of special relativity as an alternative to the use of Lorentz transformations to represent compositions of velocities. This is achieved by introducing "gyro operators"; two 3d velocity vectors are used to construct an operator, which acts on another 3d velocity.

<span class="mw-page-title-main">Unit hyperbola</span> Geometric figure

In geometry, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfy the implicit equation $In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length$

<span class="mw-page-title-main">Riemann sphere</span> Model of the extended complex plane plus a point at infinity

In mathematics, the Riemann sphere, named after Bernhard Riemann, is a model of the extended complex plane: the complex plane plus one point at infinity. This extended plane represents the extended complex numbers, that is, the complex numbers plus a value $for infinity. With the Riemann model, the point is near to very large numbers, just as the point is near to very small numbers.$

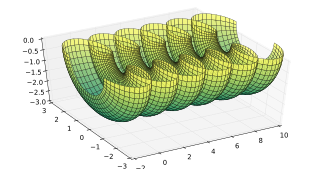
<span class="mw-page-title-main">Constant-mean-curvature surface</span>

In differential geometry, constant-mean-curvature (CMC) surfaces are surfaces with constant mean curvature. This includes minimal surfaces as a subset, but typically they are treated as special case.

References

Citations

↑ Morin, Bernard (13 November 1978). "Équations du retournement de la sphère" [Equations of the eversion of the sphere](PDF). Comptes Rendus de l'Académie des Sciences. Série A (in French). 287: 879–882.
↑ Kusner, Rob (1987). "Conformal geometry and complete minimal surfaces" (PDF). Bulletin of the American Mathematical Society. New Series. 17 (2): 291–295. doi: 10.1090/S0273-0979-1987-15564-9 ..
↑ Goodman, Sue; Marek Kossowski (2009). "Immersions of the projective plane with one triple point". Differential Geometry and Its Applications. 27 (4): 527–542. doi: 10.1016/j.difgeo.2009.01.011 . ISSN 0926-2245.
↑ Raymond O'Neil Wells (1988). "Surfaces in conformal geometry (Robert Bryant)". The Mathematical Heritage of Hermann Weyl (May 12–16, 1987, Duke University, Durham, North Carolina). Proc. Sympos. Pure Math. Vol. 48. American Mathematical Soc. pp. 227–240. doi:10.1090/pspum/048/974338. ISBN 978-0-8218-1482-6.
↑ Adam, Savage. "This Object Should've Been Impossible to Make". YouTube. Retrieved 22 June 2023.

Sources

Kirby, Rob (November 2007), "What is Boy's surface?" (PDF), Notices of the AMS, 54 (10): 1306–1307
This describes a piecewise linear model of Boy's surface.
- Casselman, Bill (November 2007), "Collapsing Boy's Umbrellas" (PDF), Notices of the AMS, 54 (10): 1356 Article on the cover illustration that accompanies the Rob Kirby article.
Mathematisches Forschungsinstitut Oberwolfach (2011), The Boy surface at Oberwolfach (PDF).
Sanderson, B. Boy's will be Boy's, (undated, 2006 or earlier).
Weisstein, Eric W. "Boy's Surface". MathWorld .

External links

Boy's surface at MathCurve; contains various visualizations, various equations, useful links and references
A planar unfolding of the Boy's surface – applet from Plus Magazine.
Boy's surface resources, including the original article, and an embedding of a topologist in the Oberwolfach Boy's surface.
A LEGO Boy's surface
A paper model of Boy's surface – pattern and instructions
Java-based model that can be freely rotated
A model of Boy's surface in Constructive Solid Geometry together with assembling instructions
Boy's surface visualization video from the Mathematical Institute of the Serbian Academy of the Arts and Sciences
This Object Should've Been Impossible to Make Adam Savage making a museum stand for a glass model of the surface

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Morin_1978-1] Morin, Bernard (13 November 1978). "Équations du retournement de la sphère" [Equations of the eversion of the sphere](PDF). Comptes Rendus de l'Académie des Sciences. Série A (in French). 287: 879–882.

[Kusner_1987-2] Kusner, Rob (1987). "Conformal geometry and complete minimal surfaces" (PDF). Bulletin of the American Mathematical Society. New Series. 17 (2): 291–295. doi: 10.1090/S0273-0979-1987-15564-9 ..

[Goodman2009-3] Goodman, Sue; Marek Kossowski (2009). "Immersions of the projective plane with one triple point". Differential Geometry and Its Applications. 27 (4): 527–542. doi: 10.1016/j.difgeo.2009.01.011 . ISSN 0926-2245.

[Wells1988-4] Raymond O'Neil Wells (1988). "Surfaces in conformal geometry (Robert Bryant)". The Mathematical Heritage of Hermann Weyl (May 12–16, 1987, Duke University, Durham, North Carolina). Proc. Sympos. Pure Math. Vol. 48. American Mathematical Soc. pp. 227–240. doi:10.1090/pspum/048/974338. ISBN 978-0-8218-1482-6.

[5] Adam, Savage. "This Object Should've Been Impossible to Make". YouTube. Retrieved 22 June 2023.

[1]

[2]

[3]

[4]

[5]