The secondary sector of the economy includes industries that produce a finished, usable product or are involved in construction.
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal transformations. Clifford algebras have important applications in a variety of fields including geometry, theoretical physics and digital image processing. They are named after the English mathematician William Kingdon Clifford.

Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and function fields. These properties, such as whether a ring admits unique factorization, the behavior of ideals, and the Galois groups of fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations.

The Crown Colony-class cruisers were a class of light cruisers of the Royal Navy named after Crown Colonies of the British Empire. The first eight are known as the Fiji class, while the last three to be built are commonly referred to as the Ceylon class and were built to a slightly modified design.

The York class was the second and final class of 8-inch (203 mm)–gunned heavy cruisers built for the Royal Navy under the terms of the 1922 Washington Naval Treaty. They were essentially a reduced version of the preceding County class, scaled down to enable more cruisers to be built from the limited defence budgets of the late 1920s.

Seeds is a cellular automaton in the same family as the Game of Life, initially investigated by Brian Silverman and named by Mirek Wójtowicz. It consists of infinite two-dimensional grid of cells, each of which may be in one of two states: on or off. Each cell is considered to have eight neighbors, as in Life. In each time step, a cell turns on or is "born" if it was off or "dead" but had exactly two neighbors that were on; all other cells turn off. Thus, in the notation describing the family of cellular automata containing Life, it is described by the rule B2/S.
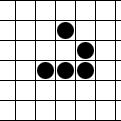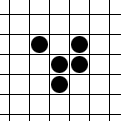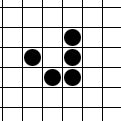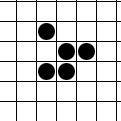
The glider is a pattern that travels across the board in Conway's Game of Life. It was first discovered by Richard K. Guy in 1970, while John Conway's group was attempting to track the evolution of the R-pentomino. Gliders are the smallest spaceships, and they travel diagonally at a speed of one cell every four generations, or . The glider is often produced from randomly generated starting configurations. John Conway has remarked that he wishes he hadn't called it the glider. The game was developed before the widespread use of interactive computers, and after seeing it animated, he feels the glider looks more like an ant walking across the plane.
The secondary armament of a battleship is composed of smaller, faster-firing weapons that are typically effective at a shorter range than the main (heavy) weapons. The nature, disposition, size and purpose of secondary weapons changed dramatically as the threat changed from torpedo boats, to torpedo-carrying destroyers, to aircraft, to anti-ship missiles.
In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann and the French mineralogist Charles-Victor Mauguin. This notation is sometimes called international notation, because it was adopted as standard by the International Tables For Crystallography since their first edition in 1935.

Biomolecular structure is the intricate folded, three-dimensional shape that is formed by a molecule of protein, DNA, or RNA, and that is important to its function. The structure of these molecules may be considered at any of several length scales ranging from the level of individual atoms to the relationships among entire protein subunits. This useful distinction among scales is often expressed as a decomposition of molecular structure into four levels: primary, secondary, tertiary, and quaternary. The scaffold for this multiscale organization of the molecule arises at the secondary level, where the fundamental structural elements are the molecule's various hydrogen bonds. This leads to several recognizable domains of protein structure and nucleic acid structure, including such secondary-structure features as alpha helixes and beta sheets for proteins, and hairpin loops, bulges, and internal loops for nucleic acids. The terms primary, secondary, tertiary, and quaternary structure were introduced by Kaj Ulrik Linderstrøm-Lang in his 1951 Lane Medical Lectures at Stanford University.
In mathematics, essential dimension is an invariant defined for certain algebraic structures such as algebraic groups and quadratic forms. It was introduced by J. Buhler and Z. Reichstein and in its most generality defined by A. Merkurjev.

The BL 6-inch Mark XII naval gun was a British 45 calibre naval gun which was mounted as primary armament on light cruisers and secondary armament on dreadnought battleships commissioned in the period 1914–1926, and remained in service on many warships until the end of World War II.

The BL 4-inch Mk IX naval gun was a British medium-velocity naval gun introduced in 1916 as secondary armament on the Renown-class battlecruisers and Glorious-class "large light cruisers", but which served most notably as the main armament on Flower-class corvettes throughout World War II.

The 75mm 50 caliber Pattern 1892 was a Russian naval gun developed in the years before the Russo-Japanese War that armed the majority of warships of the Imperial Russian Navy during the Russo-Japanese War and World War I. The majority of ships built or refit between 1890-1922 carried Pattern 1892 guns. During its career the role of the guns evolved from one of anti-torpedo boat defense to coastal artillery and anti-aircraft use.

The Canon de 65 mm Modèle 1891 & Modèle 1902 were a family of widely used naval guns of the French Navy that were also used by the Ottoman Navy during World War I. Guns removed from decommissioned ships also saw use as coastal artillery and as fortress guns in the Maginot Line fortifications during World War II.














