
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
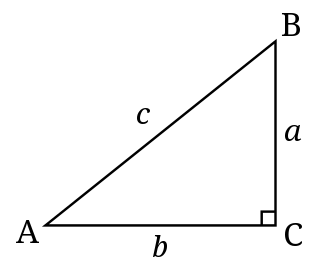
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term "oblong" is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

In geometry, two geometric objects are perpendicular if their intersection forms right angles at the point of intersection called a foot. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. Perpendicular intersections can happen between two lines, between a line and a plane, and between two planes.

In geometry and trigonometry, a right angle is an angle of exactly 90 degrees or /2 radians corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. The term is a calque of Latin angulus rectus; here rectus means "upright", referring to the vertical perpendicular to a horizontal base line.
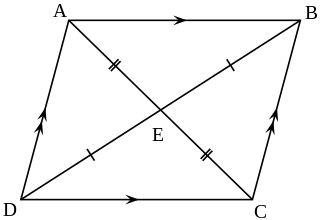
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.
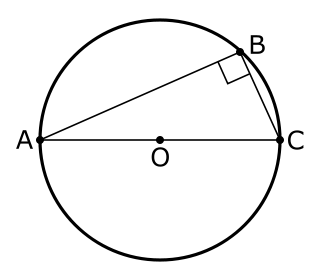
In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line AC is a diameter, the angle ∠ ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved as part of the 31st proposition in the third book of Euclid's Elements. It is generally attributed to Thales of Miletus, but it is sometimes attributed to Pythagoras.

In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of equal measure, or as a trapezoid whose diagonals have equal length. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides are parallel, and the two other sides are of equal length, and the diagonals have equal length. The base angles of an isosceles trapezoid are equal in measure.

In geometry, the statement that the angles opposite the equal sides of an isosceles triangle are themselves equal is known as the pons asinorum, typically translated as "bridge of asses". This statement is Proposition 5 of Book 1 in Euclid's Elements, and is also known as the isosceles triangle theorem. Its converse is also true: if two angles of a triangle are equal, then the sides opposite them are also equal. The term is also applied to the Pythagorean theorem.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

The following outline is provided as an overview of and topical guide to trigonometry:
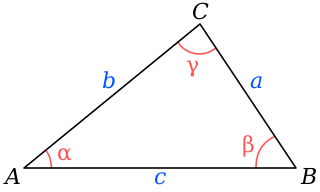
In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
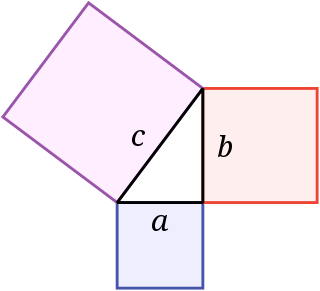
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
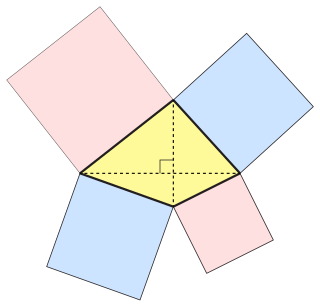
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.
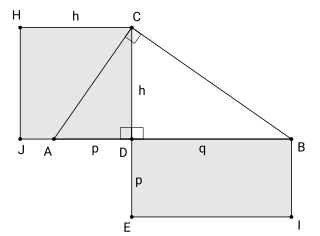
In Euclidean geometry, the right triangle altitude theorem or geometric mean theorem is a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.
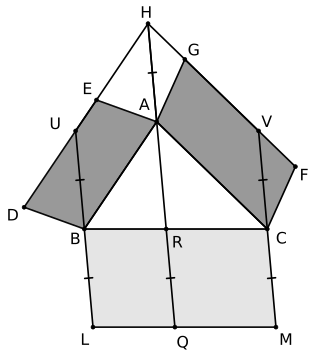
Pappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.

IM 67118, also known as Db2-146, is an Old Babylonian clay tablet in the collection of the Iraq Museum that contains the solution to a problem in plane geometry concerning a rectangle with given area and diagonal. In the last part of the text, the solution is proved correct using the Pythagorean theorem. The steps of the solution are believed to represent cut-and-paste geometry operations involving a diagram from which, it has been suggested, ancient Mesopotamians might, at an earlier time, have derived the Pythagorean theorem.

Garfield's proof of the Pythagorean theorem is an original proof the Pythagorean theorem invented by James A. Garfield, the 20th president of the United States. The proof appeared in print in the New-England Journal of Education. At the time of the publication of the proof Garfield was not the President, he was only the Congressman from Ohio. He assumed the office of President on March 4, 1881, and served in that position only for a brief period up to September 19, 1881. Garfield was the only President of the United States to have contributed anything original to mathematics. The proof is nontrivial and, according to the historian of mathematics, William Dunham, "Garfield's is really a very clever proof." The proof appears as the 231st proof in The Pythagorean Proposition, a compendium of 370 different proofs of the Pythagorean theorem.

Hsuan thu (simp. 弦图; trad. 絃圖) is a diagram given in the ancient Chinese astronomical and mathematical text Zhoubi Suanjing indicating a proof of the Pythagorean theorem. Zhoubi Suanjing is one of the oldest Chinese texts on mathematics. The exact date of composition of the book has not been determined. Some estimates of the date range as far back as 1100 BCE, while others estimate the date as late as 200 CE. However, from astronomical evidence available in the book it would appear that much of the material in the book is from the time of Confucius, that is, the 6th century BCE. Hsuan thu represents one of the earliest known proofs of the Pythagorean theorem and also one of the simplest. The text in Zhoubi Suanjing accompanying the diagram has been translated as follows:
























