Cauchy formula for repeated integration

Last updated May 14, 2024

The Cauchy formula for repeated integration, named after Augustin-Louis Cauchy, allows one to compress n antiderivatives of a function into a single integral (cf. Cauchy's formula).

Scalar case

Let f be a continuous function on the real line. Then the nth repeated integral of f with base-point a,

f^{(-n)}(x)=\int _{a}^{x}\int _{a}^{\sigma _{1}}\cdots \int _{a}^{\sigma _{n-1}}f(\sigma _{n})\,\mathrm {d} \sigma _{n}\cdots \,\mathrm {d} \sigma _{2}\,\mathrm {d} \sigma _{1},

is given by single integration

f^{(-n)}(x)={\frac {1}{(n-1)!}}\int _{a}^{x}\left(x-t\right)^{n-1}f(t)\,\mathrm {d} t.

Proof

A proof is given by induction. The base case with n=1 is trivial, since it is equivalent to:

f^{(-1)}(x)={\frac {1}{0!}}\int _{a}^{x}{(x-t)^{0}}f(t)\,\mathrm {d} t=\int _{a}^{x}f(t)\,\mathrm {d} t

Now, suppose this is true for n, and let us prove it for n+1. Firstly, using the Leibniz integral rule, note that

{\frac {\mathrm {d} }{\mathrm {d} x}}\left[{\frac {1}{n!}}\int _{a}^{x}\left(x-t\right)^{n}f(t)\,\mathrm {d} t\right]={\frac {1}{(n-1)!}}\int _{a}^{x}\left(x-t\right)^{n-1}f(t)\,\mathrm {d} t.

Then, applying the induction hypothesis,

{\begin{aligned}f^{-(n+1)}(x)&=\int _{a}^{x}\int _{a}^{\sigma _{1}}\cdots \int _{a}^{\sigma _{n}}f(\sigma _{n+1})\,\mathrm {d} \sigma _{n+1}\cdots \,\mathrm {d} \sigma _{2}\,\mathrm {d} \sigma _{1}\\&=\int _{a}^{x}\left[\int _{a}^{\sigma _{1}}\cdots \int _{a}^{\sigma _{n}}f(\sigma _{n+1})\,\mathrm {d} \sigma _{n+1}\cdots \,\mathrm {d} \sigma _{2}\right]\,\mathrm {d} \sigma _{1}\\\end{aligned}}

Note, the term within square bracket has n-times succesive integration, and upper limit of outermost integral inside the square bracket is $\sigma _{1}$ . Thus, comparing with the case for n=n, and replacing $x,\sigma _{1},\cdots ,\sigma _{n}$ of the formula at induction step n=n with $\sigma _{1},\sigma _{2},\cdots ,\sigma _{n+1}$ respectively to obtain

{\begin{aligned}\int _{a}^{\sigma _{1}}\cdots \int _{a}^{\sigma _{n}}f(\sigma _{n+1})\,\mathrm {d} \sigma _{n+1}\cdots \,\mathrm {d} \sigma _{2}&={\frac {1}{(n-1)!}}\int _{a}^{\sigma _{1}}\left(\sigma _{1}-t\right)^{n-1}f(t)\,\mathrm {d} t\\\end{aligned}}

Putting this expression inside the square bracket results in

{\begin{aligned}&=\int _{a}^{x}{\frac {1}{(n-1)!}}\int _{a}^{\sigma _{1}}\left(\sigma _{1}-t\right)^{n-1}f(t)\,\mathrm {d} t\,\mathrm {d} \sigma _{1}\\&=\int _{a}^{x}{\frac {\mathrm {d} }{\mathrm {d} \sigma _{1}}}\left[{\frac {1}{n!}}\int _{a}^{\sigma _{1}}\left(\sigma _{1}-t\right)^{n}f(t)\,\mathrm {d} t\right]\,\mathrm {d} \sigma _{1}\\&={\frac {1}{n!}}\int _{a}^{x}\left(x-t\right)^{n}f(t)\,\mathrm {d} t.\end{aligned}}

It has been shown that this statement holds true for the base case $n=1$ .
If the statement is true for $n=k$ , then it has been shown that the statement holds true for $n=k+1$ .
Thus this statement has been proven true for all positive integers.

This completes the proof.

Generalizations and applications

The Cauchy formula is generalized to non-integer parameters by the Riemann-Liouville integral, where $n\in \mathbb {Z} _{\geq 0}$ is replaced by $\alpha \in \mathbb {C} ,\ \Re (\alpha )>0$ , and the factorial is replaced by the gamma function. The two formulas agree when $\alpha \in \mathbb {Z} _{\geq 0}$ .

Both the Cauchy formula and the Riemann-Liouville integral are generalized to arbitrary dimension by the Riesz potential.

In fractional calculus, these formulae can be used to construct a differintegral, allowing one to differentiate or integrate a fractional number of times. Differentiating a fractional number of times can be accomplished by fractional integration, then differentiating the result.

Related Research Articles

In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function $f$ is a differentiable function $F$ whose derivative is equal to the original function $f$ . This can be stated symbolically as $F' = f$ . The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as $F$ and $G$ .

The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution, Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution $is the distribution of the x -intercept of a ray issuing from with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables with mean zero.$

In vector calculus and differential geometry the generalized Stokes theorem, also called the Stokes–Cartan theorem, is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. In particular, the fundamental theorem of calculus is the special case where the manifold is a line segment, Green’s theorem and Stokes' theorem are the cases of a surface in $or and the divergence theorem is the case of a volume in Hence, the theorem is sometimes referred to as the Fundamental Theorem of Multivariate Calculus .$

In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series $is said to converge absolutely if for some real number Similarly, an improper integral of a function, is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if A convergent series that is not absolutely convergent is called conditionally convergent.$

In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that, in complex analysis, "differentiation is equivalent to integration": complex differentiation, like integration, behaves well under uniform limits – a result that does not hold in real analysis.

In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of $L p$ spaces.

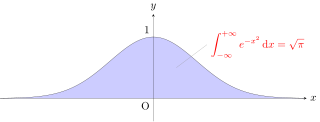
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function $over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is$

In mathematics, the Riemann–Liouville integral associates with a real function $another function Iαf of the same kind for each value of the parameter α > 0. The integral is a manner of generalization of the repeated antiderivative of f in the sense that for positive integer values of α, Iαf is an iterated antiderivative of f of order α. The Riemann–Liouville integral is named for Bernhard Riemann and Joseph Liouville, the latter of whom was the first to consider the possibility of fractional calculus in 1832. The operator agrees with the Euler transform, after Leonhard Euler, when applied to analytic functions. It was generalized to arbitrary dimensions by Marcel Riesz, who introduced the Riesz potential.$

In physics and mathematics, the Helmholtz decomposition theorem or the fundamental theorem of vector calculus states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational (curl-free) vector field and a solenoidal (divergence-free) vector field. This is named after Hermann von Helmholtz.

The Voigt profile is a probability distribution given by a convolution of a Cauchy-Lorentz distribution and a Gaussian distribution. It is often used in analyzing data from spectroscopy or diffraction.

In mathematics, the stationary phase approximation is a basic principle of asymptotic analysis, applying to functions given by integration against a rapidly-varying complex exponential.

<span class="mw-page-title-main">Itô calculus</span> Calculus of stochastic differential equations

Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion. It has important applications in mathematical finance and stochastic differential equations.

In stochastic processes, the Stratonovich integral or Fisk–Stratonovich integral is a stochastic integral, the most common alternative to the Itô integral. Although the Itô integral is the usual choice in applied mathematics, the Stratonovich integral is frequently used in physics.

In calculus, the Leibniz integral rule for differentiation under the integral sign states that for an integral of the form

In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function f of a complex argument z and an operator T, the aim is to construct an operator, f(T), which naturally extends the function f from complex argument to operator argument. More precisely, the functional calculus defines a continuous algebra homomorphism from the holomorphic functions on a neighbourhood of the spectrum of T to the bounded operators.

In mathematics, the Clark–Ocone theorem is a theorem of stochastic analysis. It expresses the value of some function F defined on the classical Wiener space of continuous paths starting at the origin as the sum of its mean value and an Itô integral with respect to that path. It is named after the contributions of mathematicians J.M.C. Clark (1970), Daniel Ocone (1984) and U.G. Haussmann (1978).

The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.

In mathematics, the Pettis integral or Gelfand–Pettis integral, named after Israel M. Gelfand and Billy James Pettis, extends the definition of the Lebesgue integral to vector-valued functions on a measure space, by exploiting duality. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure. The integral is also called the weak integral in contrast to the Bochner integral, which is the strong integral.

Stokes' theorem, also known as the Kelvin–Stokes theorem after Lord Kelvin and George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on $. Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical theorem of Stokes can be stated in one sentence: The line integral of a vector field over a loop is equal to the surface integral of its curl over the enclosed surface. It is illustrated in the figure, where the direction of positive circulation of the bounding contour \partialΣ, and the direction n of positive flux through the surface Σ, are related by a right-hand-rule. For the right hand the fingers circulate along \partialΣ and the thumb is directed along n .$

In analytic number theory, a Dirichlet series, or Dirichlet generating function (DGF), of a sequence is a common way of understanding and summing arithmetic functions in a meaningful way. A little known, or at least often forgotten about, way of expressing formulas for arithmetic functions and their summatory functions is to perform an integral transform that inverts the operation of forming the DGF of a sequence. This inversion is analogous to performing an inverse Z-transform to the generating function of a sequence to express formulas for the series coefficients of a given ordinary generating function.

References

Augustin-Louis Cauchy: Trente-Cinquième Leçon . In: Résumé des leçons données à l’Ecole royale polytechnique sur le calcul infinitésimal. Imprimerie Royale, Paris 1823. Reprint: Œuvres complètes II(4), Gauthier-Villars, Paris, pp. 5–261.
Gerald B. Folland, Advanced Calculus, p. 193, Prentice Hall (2002). ISBN 0-13-065265-2

External links

Alan Beardon (2000). "Fractional calculus II". University of Cambridge.

Maurice Mischler (2023). "About some repeated integrals and associated polynomials".

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.