In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element. More precisely, if A is a finite set of generators for G then the word problem is the membership problem for the formal language of all words in A and a formal set of inverses that map to the identity under the natural map from the free monoid with involution on A to the group G. If B is another finite generating set for G, then the word problem over the generating set B is equivalent to the word problem over the generating set A. Thus one can speak unambiguously of the decidability of the word problem for the finitely generated group G.

In mathematics, the free groupFS over a given set S consists of all words that can be built from members of S, considering two words to be different unless their equality follows from the group axioms. The members of S are called generators of FS, and the number of generators is the rank of the free group. An arbitrary group G is called free if it is isomorphic to FS for some subset S of G, that is, if there is a subset S of G such that every element of G can be written in exactly one way as a product of finitely many elements of S and their inverses.
In mathematics, a presentation is one method of specifying a group. A presentation of a group G comprises a set S of generators—so that every element of the group can be written as a product of powers of some of these generators—and a set R of relations among those generators. We then say G has presentation

In mathematics, a Cayley graph, also known as a Cayley color graph, Cayley diagram, group diagram, or color group, is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem, and uses a specified set of generators for the group. It is a central tool in combinatorial and geometric group theory. The structure and symmetry of Cayley graphs makes them particularly good candidates for constructing families of expander graphs.
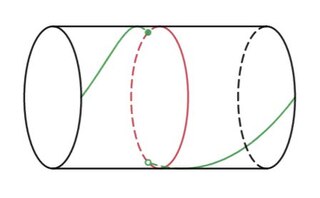
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface.

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act.

In group theory, more precisely in geometric group theory, a hyperbolic group, also known as a word hyperbolic group or Gromov hyperbolic group, is a finitely generated group equipped with a word metric satisfying certain properties abstracted from classical hyperbolic geometry. The notion of a hyperbolic group was introduced and developed by Mikhail Gromov (1987). The inspiration came from various existing mathematical theories: hyperbolic geometry but also low-dimensional topology, and combinatorial group theory. In a very influential chapter from 1987, Gromov proposed a wide-ranging research program. Ideas and foundational material in the theory of hyperbolic groups also stem from the work of George Mostow, William Thurston, James W. Cannon, Eliyahu Rips, and many others.
In computational mathematics, a word problem is the problem of deciding whether two given expressions are equivalent with respect to a set of rewriting identities. A prototypical example is the word problem for groups, but there are many other instances as well. A deep result of computational theory is that answering this question is in many important cases undecidable.
In abstract algebra, the group isomorphism problem is the decision problem of determining whether two given finite group presentations refer to isomorphic groups.
Bass–Serre theory is a part of the mathematical subject of group theory that deals with analyzing the algebraic structure of groups acting by automorphisms on simplicial trees. The theory relates group actions on trees with decomposing groups as iterated applications of the operations of free product with amalgamation and HNN extension, via the notion of the fundamental group of a graph of groups. Bass–Serre theory can be regarded as one-dimensional version of the orbifold theory.
In the mathematical subject of group theory, the rank of a groupG, denoted rank(G), can refer to the smallest cardinality of a generating set for G, that is
In the mathematical area of geometric group theory, a Van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.
In the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. Small cancellation conditions imply algebraic, geometric and algorithmic properties of the group. Finitely presented groups satisfying sufficiently strong small cancellation conditions are word hyperbolic and have word problem solvable by Dehn's algorithm. Small cancellation methods are also used for constructing Tarski monsters, and for solutions of Burnside's problem.
In the mathematical subject of geometric group theory, a Dehn function, named after Max Dehn, is an optimal function associated to a finite group presentation which bounds the area of a relation in that group in terms of the length of that relation. The growth type of the Dehn function is a quasi-isometry invariant of a finitely presented group. The Dehn function of a finitely presented group is also closely connected with non-deterministic algorithmic complexity of the word problem in groups. In particular, a finitely presented group has solvable word problem if and only if the Dehn function for a finite presentation of this group is recursive. The notion of a Dehn function is motivated by isoperimetric problems in geometry, such as the classic isoperimetric inequality for the Euclidean plane and, more generally, the notion of a filling area function that estimates the area of a minimal surface in a Riemannian manifold in terms of the length of the boundary curve of that surface.
In mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group. The motivating examples of relatively hyperbolic groups are the fundamental groups of complete noncompact hyperbolic manifolds of finite volume.
In the mathematical subject of geometric group theory, the Baumslag–Gersten group, also known as the Baumslag group, is a particular one-relator group exhibiting some remarkable properties regarding its finite quotient groups, its Dehn function and the complexity of its word problem.
In mathematics, and more precisely in topology, the mapping class group of a surface, sometimes called the modular group or Teichmüller modular group, is the group of homeomorphisms of the surface viewed up to continuous deformation. It is of fundamental importance for the study of 3-manifolds via their embedded surfaces and is also studied in algebraic geometry in relation to moduli problems for curves.
In the mathematical subject of group theory, a one-relator group is a group given by a group presentation with a single defining relation. One-relator groups play an important role in geometric group theory by providing many explicit examples of finitely presented groups.
In the mathematical subject of geometric group theory, an acylindrically hyperbolic group is a group admitting a non-elementary 'acylindrical' isometric action on some geodesic hyperbolic metric space. This notion generalizes the notions of a hyperbolic group and of a relatively hyperbolic group and includes a significantly wider class of examples, such as mapping class groups and Out(Fn).
Whitehead's algorithm is a mathematical algorithm in group theory for solving the automorphic equivalence problem in the finite rank free group Fn. The algorithm is based on a classic 1936 paper of J. H. C. Whitehead. It is still unknown if Whitehead's algorithm has polynomial time complexity.





