Related Research Articles

In physics and geometry, a catenary is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends in a uniform gravitational field.

In mechanics and physics, simple harmonic motion is a special type of periodic motion an object experiences due to a restoring force whose magnitude is directly proportional to the distance of the object from an equilibrium position and acts towards the equilibrium position. It results in an oscillation that is described by a sinusoid which continues indefinitely.
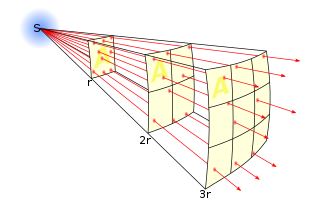
In science, an inverse-square law is any scientific law stating that the observed "intensity" of a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understood as geometric dilution corresponding to point-source radiation into three-dimensional space.

A phase diagram in physical chemistry, engineering, mineralogy, and materials science is a type of chart used to show conditions at which thermodynamically distinct phases occur and coexist at equilibrium.

Young's modulus is a mechanical property of solid materials that measures the tensile or compressive stiffness when the force is applied lengthwise. It is the modulus of elasticity for tension or axial compression. Young's modulus is defined as the ratio of the stress applied to the object and the resulting axial strain in the linear elastic region of the material.

In physics, Hooke's law is an empirical law which states that the force needed to extend or compress a spring by some distance scales linearly with respect to that distance—that is, Fs = kx, where k is a constant factor characteristic of the spring, and x is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ut tensio, sic vis. Hooke states in the 1678 work that he was aware of the law since 1660.

In engineering and materials science, a stress–strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined. These curves reveal many of the properties of a material, such as the Young's modulus, the yield strength and the ultimate tensile strength.
In physics and materials science, elasticity is the ability of a body to resist a distorting influence and to return to its original size and shape when that influence or force is removed. Solid objects will deform when adequate loads are applied to them; if the material is elastic, the object will return to its initial shape and size after removal. This is in contrast to plasticity, in which the object fails to do so and instead remains in its deformed state.

A blade is the sharp, cutting portion of a tool, weapon, or machine, specifically designed to puncture, chop, slice, or scrape surfaces or materials. Blades are typically made from materials that are harder than those they are intended to cut. This includes early examples made from flaked stones like flint or obsidian, evolving through the ages into metal forms like copper, bronze, and iron, and culminating in modern versions made from steel or ceramics. Serving as one of humanity's oldest tools, blades continue to have wide-ranging applications, including in combat, cooking, and various other everyday and specialized tasks.

A spring is a device consisting of an elastic but largely rigid material bent or molded into a form that can return into shape after being compressed or extended. Springs can store energy when compressed. In everyday use, the term most often refers to coil springs, but there are many different spring designs. Modern springs are typically manufactured from spring steel. An example of a non-metallic spring is the bow, made traditionally of flexible yew wood, which when drawn stores energy to propel an arrow.
An elastic modulus is the unit of measurement of an object's or substance's resistance to being deformed elastically when a stress is applied to it.
Solid mechanics is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.

Stiffness is the extent to which an object resists deformation in response to an applied force.

A torsion spring is a spring that works by twisting its end along its axis; that is, a flexible elastic object that stores mechanical energy when it is twisted. When it is twisted, it exerts a torque in the opposite direction, proportional to the amount (angle) it is twisted. There are various types:

A scale or balance is a device used to measure weight or mass. These are also known as mass scales, weight scales, mass balances, massometers and weight balances.

Newton's cradle is a device, usually made of metal, that demonstrates the principles of conservation of momentum and conservation of energy in physics with swinging spheres. When one sphere at the end is lifted and released, it strikes the stationary spheres, compressing them and thereby transmitting a pressure wave through the stationary spheres, which creates a force that pushes the last sphere upward. The last sphere swings back and strikes the stationary spheres, repeating the effect in the opposite direction. The device is named after 17th-century English scientist Sir Isaac Newton and was designed by French scientist Edme Mariotte. It is also known as Newton's pendulum, Newton's balls, Newton's rocker or executive ball clicker.

An anti-roll bar is an automobile suspension part that helps reduce the body roll of a vehicle during fast cornering or over road irregularities. It links opposite front or rear wheels to a torsion spring using short lever arms for anchors. This increases the suspension's roll stiffness—its resistance to roll in turns.

A balance spring, or hairspring, is a spring attached to the balance wheel in mechanical timepieces. It causes the balance wheel to oscillate with a resonant frequency when the timepiece is running, which controls the speed at which the wheels of the timepiece turn, thus the rate of movement of the hands. A regulator lever is often fitted, which can be used to alter the free length of the spring and thereby adjust the rate of the timepiece.
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed, stretched or generally deformed in any manner. Elasticity theory primarily develops formalisms for the mechanics of solid bodies and materials. The elastic potential energy equation is used in calculations of positions of mechanical equilibrium. The energy is potential as it will be converted into other forms of energy, such as kinetic energy and sound energy, when the object is allowed to return to its original shape (reformation) by its elasticity.
Structural engineering depends upon a detailed knowledge of loads, physics and materials to understand and predict how structures support and resist self-weight and imposed loads. To apply the knowledge successfully structural engineers will need a detailed knowledge of mathematics and of relevant empirical and theoretical design codes. They will also need to know about the corrosion resistance of the materials and structures, especially when those structures are exposed to the external environment.
References
- Ansel C. Ugural, Mechanical Design of Machine Components, Second Edition, page 683, CRC Press, 2015 ISBN 1439887810.