Eden's conjecture

Last updated

In the mathematics of dynamical systems, Eden's conjecture states that the supremum of the local Lyapunov dimensions on the global attractor is achieved on a stationary point or an unstable periodic orbit embedded into the attractor. [1] [2] The validity of the conjecture was proved for a number of well-known systems having global attractor (e.g. for the global attractors in the Lorenz system, [3] [4] [5] complex Ginzburg–Landau equation [6] ). It is named after Alp Eden, who proposed it in 1987.

Kuznetsov–Eden's conjecture

For local attractors, a conjecture on the Lyapunov dimension of self-excited attractor , refined by N. Kuznetsov, [7] [8] is stated that for a typical system, the Lyapunov dimension of a self-excited attractor does not exceed the Lyapunov dimension of one of the unstable equilibria, the unstable manifold of which intersects with the basin of attraction and visualizes the attractor. The conjecture is valid, e.g., for the classical self-excited Lorenz attractor; for the self-excited attractors in the Henon map (even in the case of multistability and coexistence of local attractors with different Lyapunov dimensions). [9] [10] For a hidden attractor the conjecture is that the maximum of the local Lyapunov dimensions is achieved on an unstable periodic orbit embedded into the attractor.

Related Research Articles

Chaos theory Field of mathematics

Chaos theory is an interdisciplinary scientific theory and branch of mathematics focused on underlying patterns and deterministic laws highly sensitive to initial conditions in dynamical systems that were thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnectedness, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas.

Lyapunov exponent The rate of separation of infinitesimally close trajectories

In mathematics, the Lyapunov exponent or Lyapunov characteristic exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Quantitatively, two trajectories in phase space with initial separation vector diverge at a rate given by

Attractor Concept in dynamical systems

In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed.

Hénon map

The Hénon map, sometimes called Hénon-Pomeau attractor/map, is a discrete-time dynamical system. It is one of the most studied examples of dynamical systems that exhibit chaotic behavior. The Hénon map takes a point (xn, yn) in the plane and maps it to a new point

Rabinovich–Fabrikant equations

The Rabinovich–Fabrikant equations are a set of three coupled ordinary differential equations exhibiting chaotic behaviour for certain values of the parameters. They are named after Mikhail Rabinovich and Anatoly Fabrikant, who described them in 1979.

Nonlinear control theory is the area of control theory which deals with systems that are nonlinear, time-variant, or both. Control theory is an interdisciplinary branch of engineering and mathematics that is concerned with the behavior of dynamical systems with inputs, and how to modify the output by changes in the input using feedback, feedforward, or signal filtering. The system to be controlled is called the "plant". One way to make the output of a system follow a desired reference signal is to compare the output of the plant to the desired output, and provide feedback to the plant to modify the output to bring it closer to the desired output.

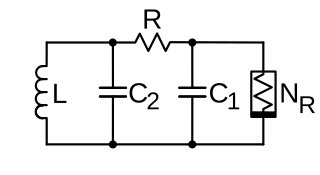
Chuas circuit

Chua's circuit is a simple electronic circuit that exhibits classic chaotic behavior. This means roughly that it is a "nonperiodic oscillator"; it produces an oscillating waveform that, unlike an ordinary electronic oscillator, never "repeats". It was invented in 1983 by Leon O. Chua, who was a visitor at Waseda University in Japan at that time. The ease of construction of the circuit has made it a ubiquitous real-world example of a chaotic system, leading some to declare it "a paradigm for chaos".

In control systems theory, the describing function (DF) method, developed by Nikolay Mitrofanovich Krylov and Nikolay Bogoliubov in the 1930s, and extended by Ralph Kochenburger is an approximate procedure for analyzing certain nonlinear control problems. It is based on quasi-linearization, which is the approximation of the non-linear system under investigation by a linear time-invariant (LTI) transfer function that depends on the amplitude of the input waveform. By definition, a transfer function of a true LTI system cannot depend on the amplitude of the input function because an LTI system is linear. Thus, this dependence on amplitude generates a family of linear systems that are combined in an attempt to capture salient features of the non-linear system behavior. The describing function is one of the few widely applicable methods for designing nonlinear systems, and is very widely used as a standard mathematical tool for analyzing limit cycles in closed-loop controllers, such as industrial process controls, servomechanisms, and electronic oscillators.

Lorenz system System of ordinary differential equations with chaotic solutions

The Lorenz system is a system of ordinary differential equations first studied by mathematician and meteorologist Edward Lorenz. It is notable for having chaotic solutions for certain parameter values and initial conditions. In particular, the Lorenz attractor is a set of chaotic solutions of the Lorenz system. In popular media the "butterfly effect" stems from the real-world implications of the Lorenz attractor, i.e. that in any physical system, in the absence of perfect knowledge of the initial conditions, our ability to predict its future course will always fail. This underscores that physical systems can be completely deterministic and yet still be inherently unpredictable even in the absence of quantum effects. The shape of the Lorenz attractor itself, when plotted graphically, may also be seen to resemble a butterfly.

In mathematics, the Markus–Yamabe conjecture is a conjecture on global asymptotic stability. If the Jacobian matrix of a dynamical system at a fixed point is Hurwitz, then the fixed point is asymptotically stable. Markus-Yamabe conjecture asks if a similar result holds globally. Precisely, the conjecture states that if a continuously differentiable map on an -dimensional real vector space has a fixed point, and its Jacobian matrix is everywhere Hurwitz, then the fixed point is globally stable.

In nonlinear control, Aizerman's conjecture or Aizerman problem states that a linear system in feedback with a sector nonlinearity would be stable if the linear system is stable for any linear gain of the sector. This conjecture was proven false but led to the (valid) sufficient criteria on absolute stability.

A coupled map lattice (CML) is a dynamical system that models the behavior of non-linear systems. They are predominantly used to qualitatively study the chaotic dynamics of spatially extended systems. This includes the dynamics of spatiotemporal chaos where the number of effective degrees of freedom diverges as the size of the system increases.

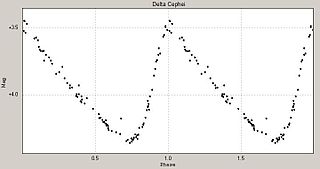
Stellar pulsation

Stellar pulsations are caused by expansions and contractions in the outer layers as a star seeks to maintain equilibrium. These fluctuations in stellar radius cause corresponding changes in the luminosity of the star. Astronomers are able to deduce this mechanism by measuring the spectrum and observing the Doppler effect. Many intrinsic variable stars that pulsate with large amplitudes, such as the classical Cepheids, RR Lyrae stars and large-amplitude Delta Scuti stars show regular light curves.

In the bifurcation theory, a bounded oscillation that is born without loss of stability of stationary set is called a hidden oscillation. In nonlinear control theory, the birth of a hidden oscillation in a time-invariant control system with bounded states means crossing a boundary, in the domain of the parameters, where local stability of the stationary states implies global stability. If a hidden oscillation attracts all nearby oscillations, then it is called a hidden attractor. For a dynamical system with a unique equilibrium point that is globally attractive, the birth of a hidden attractor corresponds to a qualitative change in behaviour from monostability to bi-stability. In the general case, a dynamical system may turn out to be multistable and have coexisting local attractors in the phase space. While trivial attractors, i.e. stable equilibrium points, can be easily found analytically or numerically, the search of periodic and chaotic attractors can turn out to be a challenging problem.

Kalman's conjecture or Kalman problem is a disproved conjecture on absolute stability of nonlinear control system with one scalar nonlinearity, which belongs to the sector of linear stability. Kalman's conjecture is a strengthening of Aizerman's conjecture and is a special case of Markus–Yamabe conjecture. This conjecture was proven false but led to the (valid) sufficient criteria on absolute stability.

In applied mathematics, the Kaplan–Yorke conjecture concerns the dimension of an attractor, using Lyapunov exponents. By arranging the Lyapunov exponents in order from largest to smallest , let j be the index for which

In the mathematics of dynamical systems, the concept of Lyapunov dimension was suggested by Kaplan and Yorke for estimating the Hausdorff dimension of attractors. Further the concept has been developed and rigorously justified in a number of papers, and nowadays various different approaches to the definition of Lyapunov dimension are used. Remark that the attractors with noninteger Hausdorff dimension are called strange attractors. Since the direct numerical computation of the Hausdorff dimension of attractors is often a problem of high numerical complexity, estimations via the Lyapunov dimension became widely spread. The Lyapunov dimension was named after the Russian mathematician Aleksandr Lyapunov because of the close connection with the Lyapunov exponents.

Nikolay Vladimirovich Kuznetsov is a Russian scientist, specialist in nonlinear dynamics and control theory.

In mechanics, Sommerfeld effect is a phenomenon arising from feedback in the energy exchange between vibrating systems: for example, when for the rocking table, under given conditions, energy transmitted to the motor resulted not in higher revolutions but in stronger vibrations of the table. It is named after Arnold Sommerfeld. In 1902, A. Sommerfeld analyzed the vibrations caused by a motor driving an unbalanced weight and wrote that "This experiment corresponds roughly to the case in which a factory owner has a machine set on a poor foundation running at 30 horsepower. He achieves an effective level of just 1/3, however, because only 10 horsepower are doing useful work, while 20 horsepower are transferred to the foundational masonry". First mathematical descriptions of Sommerfeld effect were suggested by I. Blekhman and V. Konenko.

William F. Egan is an expert and author in the area of PLLs. The first and second editions of his book Frequency Synthesis by Phase Lock as well as his book Phase-Lock Basics are references among electrical engineers specializing in areas involving PLLs.

References

  1. ↑ A. Eden (1989). An abstract theory of L-exponents with applications to dimension analysis. PhD thesis. Indiana University.
  2. ↑ Eden, A. (1989). "Local Lyapunov exponents and a local estimate of Hausdorff dimension". Modélisation Mathématique et Analyse Numérique. 23 (3): 405–413. doi: 10.1051/m2an/1989230304051 .
  3. ↑ Leonov, G.; Lyashko, S. (1993). "Eden's hypothesis for a Lorenz system". Vestn. St. Petersbg. Univ., Math. 26 (3): 15–18.
  4. ↑ Leonov, G.A.; Kuznetsov, N.V.; Korzhemanova, N.A.; Kusakin, D.V. (2016). "Lyapunov dimension formula for the global attractor of the Lorenz system". Communications in Nonlinear Science and Numerical Simulation. 41: 84–103. arXiv: 1508.07498 . Bibcode:2016CNSNS..41...84L. doi:10.1016/j.cnsns.2016.04.032. S2CID   119614076.
  5. ↑ Kuznetsov, N.V.; Mokaev, T.N.; Kuznetsova, O.A.; Kudryashova, E.V. (2020). "The Lorenz system: hidden boundary of practical stability and the Lyapunov dimension". Nonlinear Dynamics. 102 (2): 713–732. doi: 10.1007/s11071-020-05856-4 .
  6. ↑ Doering, C.R.; Gibbon, J.D.; Holm, D.D.; Nicolaenko, B. (1987). "Exact Lyapunov dimension of the universal attractor for the complex Ginzburg–Landau equation". Physical Review Letters. 59 (26): 2911–2914. Bibcode:1987PhRvL..59.2911D. doi:10.1103/physrevlett.59.2911. PMID   10035685.
  7. ↑ Kuznetsov, N.V. (2016). "The Lyapunov dimension and its estimation via the Leonov method". Physics Letters A. 380 (25–26): 2142–2149. arXiv: 1602.05410 . Bibcode:2016PhLA..380.2142K. doi:10.1016/j.physleta.2016.04.036. S2CID   118467839.
  8. ↑ Kuznetsov, N.V.; Leonov, G.A.; Mokaev, T.N.; Prasad, A.; Shrimali, M.D. (2018). "Finite-time Lyapunov dimension and hidden attractor of the Rabinovich system". Nonlinear Dynamics. 92 (2): 267–285. arXiv: 1504.04723 . doi:10.1007/s11071-018-4054-z. S2CID   54706479.
  9. ↑ Kuznetsov, N.V.; Leonov, G.A.; Mokaev, T.N. (2017). "Finite-time and exact Lyapunov dimension of the Henon map". arXiv: 1712.01270 [nlin.CD].
  10. ↑ Kuznetsov, Nikolay; Reitmann, Volker (2021). Attractor Dimension Estimates for Dynamical Systems: Theory and Computation. Cham: Springer.


This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.