In mathematics, a partition of unity of a topological space is a set of continuous functions from to the unit interval [0,1] such that for every point :

Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

In particle physics, Fermi's interaction is an explanation of the beta decay, proposed by Enrico Fermi in 1933. The theory posits four fermions directly interacting with one another. This interaction explains beta decay of a neutron by direct coupling of a neutron with an electron, a neutrino and a proton.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics.
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.
In mathematical logic, Heyting arithmetic is an axiomatization of arithmetic in accordance with the philosophy of intuitionism. It is named after Arend Heyting, who first proposed it.
In theoretical physics, Seiberg–Witten theory is an supersymmetric gauge theory with an exact low-energy effective action, of which the kinetic part coincides with the Kähler potential of the moduli space of vacua. Before taking the low-energy effective action, the theory is known as supersymmetric Yang–Mills theory, as the field content is a single vector supermultiplet, analogous to the field content of Yang–Mills theory being a single vector gauge field or connection.

Toroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that separates its two foci. Thus, the two foci and in bipolar coordinates become a ring of radius in the plane of the toroidal coordinate system; the -axis is the axis of rotation. The focal ring is also known as the reference circle.
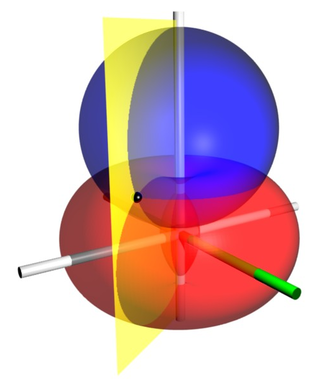
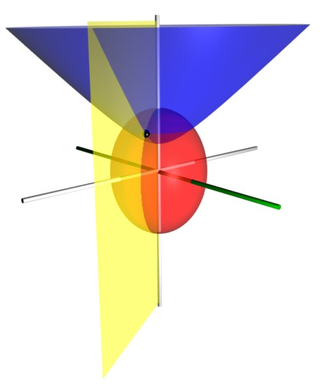
Bispherical coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that connects the two foci. Thus, the two foci and in bipolar coordinates remain points in the bispherical coordinate system.

Elliptic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional elliptic coordinate system in the perpendicular -direction. Hence, the coordinate surfaces are prisms of confocal ellipses and hyperbolae. The two foci and are generally taken to be fixed at and , respectively, on the -axis of the Cartesian coordinate system.
Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the focal axis of the ellipse, i.e., the symmetry axis on which the foci are located. Rotation about the other axis produces oblate spheroidal coordinates. Prolate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two smallest principal axes are equal in length.

Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of radius in the x-y plane. Oblate spheroidal coordinates can also be considered as a limiting case of ellipsoidal coordinates in which the two largest semi-axes are equal in length.
The Newman–Penrose (NP) formalism is a set of notation developed by Ezra T. Newman and Roger Penrose for general relativity (GR). Their notation is an effort to treat general relativity in terms of spinor notation, which introduces complex forms of the usual variables used in GR. The NP formalism is itself a special case of the tetrad formalism, where the tensors of the theory are projected onto a complete vector basis at each point in spacetime. Usually this vector basis is chosen to reflect some symmetry of the spacetime, leading to simplified expressions for physical observables. In the case of the NP formalism, the vector basis chosen is a null tetrad: a set of four null vectors—two real, and a complex-conjugate pair. The two real members often asymptotically point radially inward and radially outward, and the formalism is well adapted to treatment of the propagation of radiation in curved spacetime. The Weyl scalars, derived from the Weyl tensor, are often used. In particular, it can be shown that one of these scalars— in the appropriate frame—encodes the outgoing gravitational radiation of an asymptotically flat system.
In mathematics, the theory of optimal stopping or early stopping is concerned with the problem of choosing a time to take a particular action, in order to maximise an expected reward or minimise an expected cost. Optimal stopping problems can be found in areas of statistics, economics, and mathematical finance. A key example of an optimal stopping problem is the secretary problem. Optimal stopping problems can often be written in the form of a Bellman equation, and are therefore often solved using dynamic programming.
In constructive mathematics, Church's thesis is an axiom stating that all total functions are computable functions.
In artificial intelligence and related fields, an argumentation framework is a way to deal with contentious information and draw conclusions from it using formalized arguments.
Variable elimination (VE) is a simple and general exact inference algorithm in probabilistic graphical models, such as Bayesian networks and Markov random fields. It can be used for inference of maximum a posteriori (MAP) state or estimation of conditional or marginal distributions over a subset of variables. The algorithm has exponential time complexity, but could be efficient in practice for low-treewidth graphs, if the proper elimination order is used.
In mathematical logic, the intersection type discipline is a branch of type theory encompassing type systems that use the intersection type constructor to assign multiple types to a single term. In particular, if a term can be assigned both the type and the type , then can be assigned the intersection type . Therefore, the intersection type constructor can be used to express finite heterogeneous ad hoc polymorphism . For example, the λ-term can be assigned the type in most intersection type systems, assuming for the term variable both the function type and the corresponding argument type .
In theoretical physics, more specifically in quantum field theory and supersymmetry, supersymmetric Yang–Mills, also known as super Yang–Mills and abbreviated to SYM, is a supersymmetric generalization of Yang–Mills theory, which is a gauge theory that plays an important part in the mathematical formulation of forces in particle physics.


































