
Benoit B.Mandelbrot was a Polish-born French-American mathematician and polymath with broad interests in the practical sciences, especially regarding what he labeled as "the art of roughness" of physical phenomena and "the uncontrolled element in life". He referred to himself as a "fractalist" and is recognized for his contribution to the field of fractal geometry, which included coining the word "fractal", as well as developing a theory of "roughness and self-similarity" in nature.

In physics and mathematics, the dimension of a mathematical space is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordinate is needed to specify a point on it – for example, the point at 5 on a number line. A surface, such as the boundary of a cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on it – for example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces.
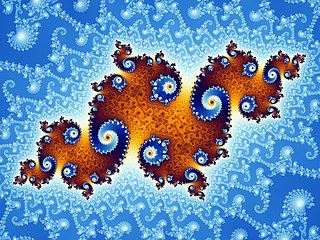
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.

Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still digital images, animations, and media. Fractal art developed from the mid-1980s onwards. It is a genre of computer art and digital art which are part of new media art. The mathematical beauty of fractals lies at the intersection of generative art and computer art. They combine to produce a type of abstract art.

Fractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image. Fractal algorithms convert these parts into mathematical data called "fractal codes" which are used to recreate the encoded image.

A fractal landscape or fractal surface is generated using a stochastic algorithm designed to produce fractal behavior that mimics the appearance of natural terrain. In other words, the surface resulting from the procedure is not a deterministic, but rather a random surface that exhibits fractal behavior.
In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.

In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set in a Euclidean space , or more generally in a metric space . It is named after the Polish mathematician Hermann Minkowski and the French mathematician Georges Bouligand.

Diffusion-limited aggregation (DLA) is the process whereby particles undergoing a random walk due to Brownian motion cluster together to form aggregates of such particles. This theory, proposed by T.A. Witten Jr. and L.M. Sander in 1981, is applicable to aggregation in any system where diffusion is the primary means of transport in the system. DLA can be observed in many systems such as electrodeposition, Hele-Shaw flow, mineral deposits, and dielectric breakdown.

In mathematics, the term chaos game originally referred to a method of creating a fractal, using a polygon and an initial point selected at random inside it. The fractal is created by iteratively creating a sequence of points, starting with the initial random point, in which each point in the sequence is a given fraction of the distance between the previous point and one of the vertices of the polygon; the vertex is chosen at random in each iteration. Repeating this iterative process a large number of times, selecting the vertex at random on each iteration, and throwing out the first few points in the sequence, will often produce a fractal shape. Using a regular triangle and the factor 1/2 will result in the Sierpinski triangle, while creating the proper arrangement with four points and a factor 1/2 will create a display of a "Sierpinski Tetrahedron", the three-dimensional analogue of the Sierpinski triangle. As the number of points is increased to a number N, the arrangement forms a corresponding (N-1)-dimensional Sierpinski Simplex.
Chaos or CHAOS may refer to:

Algorithmic art or algorithm art is art, mostly visual art, in which the design is generated by an algorithm. Algorithmic artists are sometimes called algorists.

The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal curve–like properties of coastlines; i.e., the fact that a coastline typically has a fractal dimension. Although the "paradox of length" was previously noted by Hugo Steinhaus, the first systematic study of this phenomenon was by Lewis Fry Richardson, and it was expanded upon by Benoit Mandelbrot.
A T-square is a drafting and technical drawing tool.

A scenery generator is software used to create landscape images, 3D models, and animations. These programs often use procedural generation to generate the landscapes. If not using procedural generation to create the landscapes, then normally a 3D artist would render and create the landscapes. These programs are often used in video games or movies. Basic elements of landscapes created by scenery generators include terrain, water, foliage, and clouds. The process for basic random generation uses a diamond square algorithm.
In physical cosmology, fractal cosmology is a set of minority cosmological theories which state that the distribution of matter in the Universe, or the structure of the universe itself, is a fractal across a wide range of scales. More generally, it relates to the usage or appearance of fractals in the study of the universe and matter. A central issue in this field is the fractal dimension of the universe or of matter distribution within it, when measured at very large or very small scales.
Fractal analysis is assessing fractal characteristics of data. It consists of several methods to assign a fractal dimension and other fractal characteristics to a dataset which may be a theoretical dataset, or a pattern or signal extracted from phenomena including topography, natural geometric objects, ecology and aquatic sciences, sound, market fluctuations, heart rates, frequency domain in electroencephalography signals, digital images, molecular motion, and data science. Fractal analysis is now widely used in all areas of science. An important limitation of fractal analysis is that arriving at an empirically determined fractal dimension does not necessarily prove that a pattern is fractal; rather, other essential characteristics have to be considered. Fractal analysis is valuable in expanding our knowledge of the structure and function of various systems, and as a potential tool to mathematically assess novel areas of study. Fractal calculus was formulated which is a generalization of ordinary calculus.

Fractal-generating software is any type of graphics software that generates images of fractals. There are many fractal generating programs available, both free and commercial. Mobile apps are available to play or tinker with fractals. Some programmers create fractal software for themselves because of the novelty and because of the challenge in understanding the related mathematics. The generation of fractals has led to some very large problems for pure mathematics.

Computer-generated imagery (CGI) is a specific-technology or application of computer graphics for creating or improving images in art, printed media, simulators, videos and video games. These images are either static or dynamic. CGI both refers to 2D computer graphics and 3D computer graphics with the purpose of designing characters, virtual worlds, or scenes and special effects. The application of CGI for creating/improving animations is called computer animation, or CGI animation.













