Related Research Articles

A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. A deterministic finite-state machine can be constructed equivalent to any non-deterministic one.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
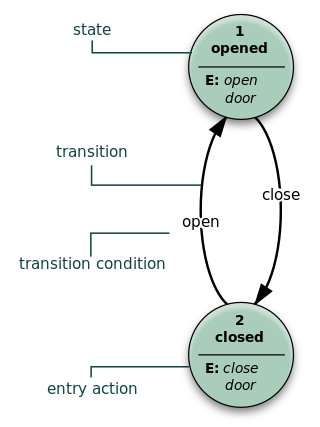
A state diagram is a type of diagram used in computer science and related fields to describe the behavior of systems. State diagrams require that the system described is composed of a finite number of states; sometimes, this is indeed the case, while at other times this is a reasonable abstraction. Many forms of state diagrams exist, which differ slightly and have different semantics.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In theoretical computer science, more precisely in the theory of formal languages, the star height is a measure for the structural complexity of regular expressions and regular languages. The star height of a regular expression equals the maximum nesting depth of stars appearing in that expression. The star height of a regular language is the least star height of any regular expression for that language. The concept of star height was first defined and studied by Eggan (1963).
In automata theory, an alternating finite automaton (AFA) is a nondeterministic finite automaton whose transitions are divided into existential and universal transitions. For example, let A be an alternating automaton.
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines relations between sets of strings.
In the theory of computation and automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton (NFA) into a deterministic finite automaton (DFA) which recognizes the same formal language. It is important in theory because it establishes that NFAs, despite their additional flexibility, are unable to recognize any language that cannot be recognized by some DFA. It is also important in practice for converting easier-to-construct NFAs into more efficiently executable DFAs. However, if the NFA has n states, the resulting DFA may have up to 2n states, an exponentially larger number, which sometimes makes the construction impractical for large NFAs.
In computer science, in particular in automata theory, a two-way finite automaton is a finite automaton that is allowed to re-read its input.
In quantum computing, quantum finite automata (QFA) or quantum state machines are a quantum analog of probabilistic automata or a Markov decision process. They provide a mathematical abstraction of real-world quantum computers. Several types of automata may be defined, including measure-once and measure-many automata. Quantum finite automata can also be understood as the quantization of subshifts of finite type, or as a quantization of Markov chains. QFAs are, in turn, special cases of geometric finite automata or topological finite automata.
In mathematics and computer science, the probabilistic automaton (PA) is a generalization of the nondeterministic finite automaton; it includes the probability of a given transition into the transition function, turning it into a transition matrix. Thus, the probabilistic automaton also generalizes the concepts of a Markov chain and of a subshift of finite type. The languages recognized by probabilistic automata are called stochastic languages; these include the regular languages as a subset. The number of stochastic languages is uncountable.

In automata theory, DFA minimization is the task of transforming a given deterministic finite automaton (DFA) into an equivalent DFA that has a minimum number of states. Here, two DFAs are called equivalent if they recognize the same regular language. Several different algorithms accomplishing this task are known and described in standard textbooks on automata theory.
In automata theory, a branch of theoretical computer science, an ω-automaton is a variation of finite automata that runs on infinite, rather than finite, strings as input. Since ω-automata do not stop, they have a variety of acceptance conditions rather than simply a set of accepting states.
In computer science, Thompson's construction algorithm, also called the McNaughton–Yamada–Thompson algorithm, is a method of transforming a regular expression into an equivalent nondeterministic finite automaton (NFA). This NFA can be used to match strings against the regular expression. This algorithm is credited to Ken Thompson.
In computational learning theory, induction of regular languages refers to the task of learning a formal description of a regular language from a given set of example strings. Although E. Mark Gold has shown that not every regular language can be learned this way, approaches have been investigated for a variety of subclasses. They are sketched in this article. For learning of more general grammars, see Grammar induction.
In theoretical computer science, in particular in formal language theory, Kleene's algorithm transforms a given nondeterministic finite automaton (NFA) into a regular expression. Together with other conversion algorithms, it establishes the equivalence of several description formats for regular languages. Alternative presentations of the same method include the "elimination method" attributed to Brzozowski and McCluskey, the algorithm of McNaughton and Yamada, and the use of Arden's lemma.
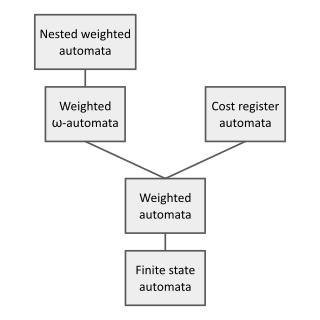
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.
In automata theory, an unambiguous finite automaton (UFA) is a nondeterministic finite automaton (NFA) such that each word has at most one accepting path. Each deterministic finite automaton (DFA) is an UFA, but not vice versa. DFA, UFA, and NFA recognize exactly the same class of formal languages. On the one hand, an NFA can be exponentially smaller than an equivalent DFA. On the other hand, some problems are easily solved on DFAs and not on UFAs. For example, given an automaton A, an automaton A′ which accepts the complement of A can be computed in linear time when A is a DFA, it is not known whether it can be done in polynomial time for UFA. Hence UFAs are a mix of the worlds of DFA and of NFA; in some cases, they lead to smaller automata than DFA and quicker algorithms than NFA.
References
- Yo-Sub Han and Derick Wood. "The Generalization of Generalized Automata: Expression Automata." In: 9th International Conference on Implementation and Application of Automata, CIAA 2004, Kingston, Canada, July 22–24, 2004, Revised Selected Papers, LNCS 3317, pp. 156–166. doi : 10.1007/b105090
- Michael Sipser. 2006. Introduction to the Theory of Computation (2nd ed.). International Thomson Publishing.