
In computational geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points.

In computational geometry, the gift wrapping algorithm is an algorithm for computing the convex hull of a given set of points.
In the two-dimensional case the algorithm is also known as Jarvis march, after R. A. Jarvis, who published it in 1973; it has O(nh) time complexity, where n is the number of points and h is the number of points on the convex hull. Its real-life performance compared with other convex hull algorithms is favorable when n is small or h is expected to be very small with respect to n[ citation needed ]. In general cases, the algorithm is outperformed by many others [ example needed ][ citation needed ].
For the sake of simplicity, the description below assumes that the points are in general position, i.e., no three points are collinear. The algorithm may be easily modified to deal with collinearity, including the choice whether it should report only extreme points (vertices of the convex hull) or all points that lie on the convex hull[ citation needed ]. Also, the complete implementation must deal[ how? ] with degenerate cases when the convex hull has only 1 or 2 vertices, as well as with the issues of limited arithmetic precision, both of computer computations and input data.
The gift wrapping algorithm begins with i=0 and a point p0 known to be on the convex hull, e.g., the leftmost point, and selects the point pi+1 such that all points are to the right of the line pi pi+1. This point may be found in O(n) time by comparing polar angles of all points with respect to point pi taken for the center of polar coordinates. Letting i=i+1, and repeating with until one reaches ph=p0 again yields the convex hull in h steps. In two dimensions, the gift wrapping algorithm is similar to the process of winding a string (or wrapping paper) around the set of points.
The approach can be extended to higher dimensions.

algorithm jarvis(S) is // S is the set of points // P will be the set of points which form the convex hull. Final set size is i. pointOnHull = leftmost point in S // which is guaranteed to be part of the CH(S) i := 0 repeat P[i] := pointOnHull endpoint := S[0] // initial endpoint for a candidate edge on the hull for j from 0 to |S| do // endpoint == pointOnHull is a rare case and can happen only when j == 1 and a better endpoint has not yet been set for the loop if (endpoint == pointOnHull) or (S[j] is on left of line from P[i] to endpoint) then endpoint := S[j] // found greater left turn, update endpoint i := i + 1 pointOnHull = endpoint until endpoint = P[0] // wrapped around to first hull point
The inner loop checks every point in the set S, and the outer loop repeats for each point on the hull. Hence the total run time is . The run time depends on the size of the output, so Jarvis's march is an output-sensitive algorithm.
However, because the running time depends linearly on the number of hull vertices, it is only faster than algorithms such as Graham scan when the number h of hull vertices is smaller than log n. Chan's algorithm, another convex hull algorithm, combines the logarithmic dependence of Graham scan with the output sensitivity of the gift wrapping algorithm, achieving an asymptotic running time that improves on both Graham scan and gift wrapping.

In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.

In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset.
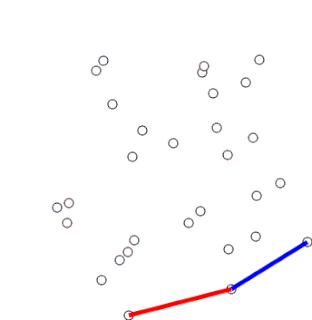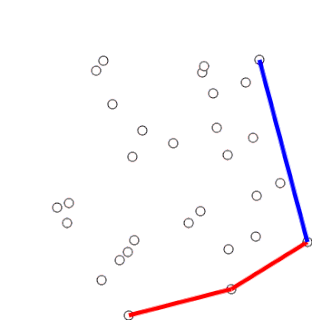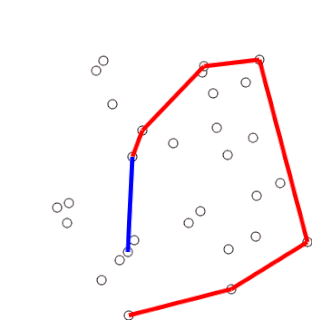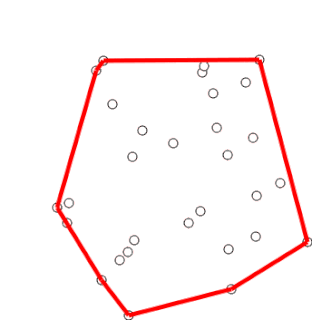
Graham's scan is a method of finding the convex hull of a finite set of points in the plane with time complexity O(n log n). It is named after Ronald Graham, who published the original algorithm in 1972. The algorithm finds all vertices of the convex hull ordered along its boundary. It uses a stack to detect and remove concavities in the boundary efficiently.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
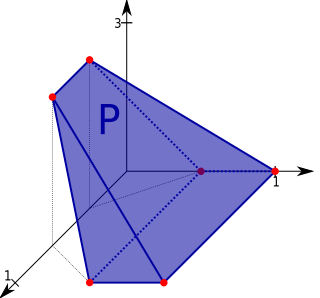
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn. Some authors use the terms "convex polytope" and "convex polyhedron" interchangeably, while others prefer to draw a distinction between the notions of a polyhedron and a polytope.
In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left. If in the above definition one interchanges left and right, one obtains a negatively oriented curve.

In computational geometry, Chan's algorithm, named after Timothy M. Chan, is an optimal output-sensitive algorithm to compute the convex hull of a set of points, in 2- or 3-dimensional space. The algorithm takes time, where is the number of vertices of the output. In the planar case, the algorithm combines an algorithm with Jarvis march, in order to obtain an optimal time. Chan's algorithm is notable because it is much simpler than the Kirkpatrick–Seidel algorithm, and it naturally extends to 3-dimensional space. This paradigm has been independently developed by Frank Nielsen in his Ph.D. thesis.
The dynamic convex hull problem is a class of dynamic problems in computational geometry. The problem consists in the maintenance, i.e., keeping track, of the convex hull for input data undergoing a sequence of discrete changes, i.e., when input data elements may be inserted, deleted, or modified. It should be distinguished from the kinetic convex hull, which studies similar problems for continuously moving points. Dynamic convex hull problems may be distinguished by the types of the input data and the allowed types of modification of the input data.
The Kirkpatrick–Seidel algorithm, proposed by its authors as a potential "ultimate planar convex hull algorithm", is an algorithm for computing the convex hull of a set of points in the plane, with time complexity, where is the number of input points and is the number of points in the hull. Thus, the algorithm is output-sensitive: its running time depends on both the input size and the output size. Another output-sensitive algorithm, the gift wrapping algorithm, was known much earlier, but the Kirkpatrick–Seidel algorithm has an asymptotic running time that is significantly smaller and that always improves on the bounds of non-output-sensitive algorithms. The Kirkpatrick–Seidel algorithm is named after its inventors, David G. Kirkpatrick and Raimund Seidel.
Algorithms that construct convex hulls of various objects have a broad range of applications in mathematics and computer science.

In computational geometry, the visibility polygon or visibility region for a point p in the plane among obstacles is the possibly unbounded polygonal region of all points of the plane visible from p. The visibility polygon can also be defined for visibility from a segment, or a polygon. Visibility polygons are useful in robotics, video games, and in determining positions to locate facilities, such as the best placement of security guards in an art gallery.
In computational geometry, the smallest enclosing box problem is that of finding the oriented minimum bounding box enclosing a set of points. It is a type of bounding volume. "Smallest" may refer to volume, area, perimeter, etc. of the box.
In computer science, an output-sensitive algorithm is an algorithm whose running time depends on the size of the output, instead of, or in addition to, the size of the input. For certain problems where the output size varies widely, for example from linear in the size of the input to quadratic in the size of the input, analyses that take the output size explicitly into account can produce better runtime bounds that differentiate algorithms that would otherwise have identical asymptotic complexity.
In computer science, a segment tree, also known as a statistic tree, is a tree data structure used for storing information about intervals, or segments. It allows querying which of the stored segments contain a given point. It is, in principle, a static structure; that is, it's a structure that cannot be modified once it's built. A similar data structure is the interval tree.
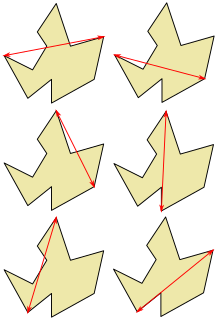
In computational geometry, the method of rotating calipers is an algorithm design technique that can be used to solve optimization problems including finding the width or diameter of a set of points.

Quickhull is a method of computing the convex hull of a finite set of points in n-dimensional space. It uses a divide and conquer approach similar to that of quicksort, from which its name derives. Its worst case complexity for 2-dimensional and 3-dimensional space is considered to be , where is the number of input points and is the number of processed points. However, unlike quicksort, there is no obvious way to convert quickhull into a randomized algorithm. Thus, its average time complexity cannot be easily calculated.
A kinetic convex hull data structure is a kinetic data structure that maintains the convex hull of a set of continuously moving points. It should be distinguished from dynamic convex hull data structures, which handle points undergoing discrete changes such as insertions or deletions of points rather than continuous motion.
A kinetic diameter data structure is a kinetic data structure which maintains the diameter of a set of moving points. The diameter of a set of moving points is the maximum distance between any pair of points in the set. In the two dimensional case, the kinetic data structure for kinetic convex hull can be used to construct a kinetic data structure for the diameter of a moving point set that is responsive, compact and efficient.
A kinetic width data structure is a kinetic data structure which maintains the width of a set of moving points. In 2D, the width of a point set is the minimum distance between two parallel lines that contain the point set in the strip between them. For the two dimensional case, the kinetic data structure for kinetic convex hull can be used to construct a kinetic data structure for the width of a point set that is responsive, compact and efficient.