A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
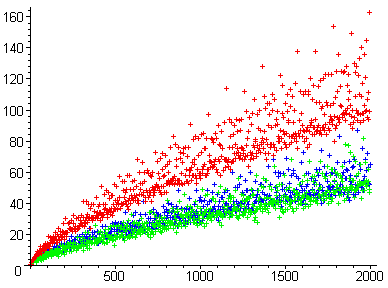
In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.

In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic that gives conditions for the solvability of quadratic equations modulo prime numbers. Due to its subtlety, it has many formulations, but the most standard statement is:
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair. In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term twin prime is used for a pair of twin primes; an alternative name for this is prime twin or prime pair.

Goldbach's conjecture is one of the oldest and best-known unsolved problems in number theory and all of mathematics. It states that every even natural number greater than 2 is the sum of two prime numbers.

In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as . This integral domain is a particular case of a commutative ring of quadratic integers. It does not have a total ordering that respects arithmetic.

In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as or , and may also be called Euler's phi function. In other words, it is the number of integers k in the range 1 ≤ k ≤ n for which the greatest common divisor gcd(n, k) is equal to 1. The integers k of this form are sometimes referred to as totatives of n.

The Ulam spiral or prime spiral is a graphical depiction of the set of prime numbers, devised by mathematician Stanisław Ulam in 1963 and popularized in Martin Gardner's Mathematical Games column in Scientific American a short time later. It is constructed by writing the positive integers in a square spiral and specially marking the prime numbers.
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these L-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case.
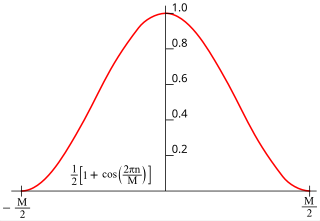
In signal processing and statistics, a window function is a mathematical function that is zero-valued outside of some chosen interval, normally symmetric around the middle of the interval, usually near a maximum in the middle, and usually tapering away from the middle. Mathematically, when another function or waveform/data-sequence is "multiplied" by a window function, the product is also zero-valued outside the interval: all that is left is the part where they overlap, the "view through the window". Equivalently, and in actual practice, the segment of data within the window is first isolated, and then only that data is multiplied by the window function values. Thus, tapering, not segmentation, is the main purpose of window functions.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form

In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Peter Gustav Lejeune Dirichlet's 1837 introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions. It is well known for its results on prime numbers and additive number theory.
In mathematics, in the area of number theory, a Gaussian period is a certain kind of sum of roots of unity. The periods permit explicit calculations in cyclotomic fields connected with Galois theory and with harmonic analysis. They are basic in the classical theory called cyclotomy. Closely related is the Gauss sum, a type of exponential sum which is a linear combination of periods.
In additive number theory, Fermat's theorem on sums of two squares states that an odd prime p can be expressed as:
In mathematics, a Kloosterman sum is a particular kind of exponential sum. They are named for the Dutch mathematician Hendrik Kloosterman, who introduced them in 1926 when he adapted the Hardy–Littlewood circle method to tackle a problem involving positive definite diagonal quadratic forms in four as opposed to five or more variables, which he had dealt with in his dissertation in 1924.
Cubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p (mod q) is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the ring of Eisenstein integers, both coprime to 3, the congruence x3 ≡ p is solvable if and only if x3 ≡ q is solvable.
In number theory, a prime k-tuple is a finite collection of values representing a repeatable pattern of differences between prime numbers. For a k-tuple (a, b, …), the positions where the k-tuple matches a pattern in the prime numbers are given by the set of integers n such that all of the values (n + a, n + b, …) are prime. Typically the first value in the k-tuple is 0 and the rest are distinct positive even numbers.

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the congruence x4 ≡ p to that of x4 ≡ q.