
In mathematics, a normed vector space is a vector space over the real or complex numbers, on which a norm is defined. A norm is the formalization and the generalization to real vector spaces of the intuitive notion of distance in the real world. A norm is a real-valued function defined on the vector space that has the following properties:
- The zero vector, 0, has zero length; every other vector has a positive length.
- Multiplying a vector by a positive number changes its length without changing its direction. Moreover,
- The triangle inequality holds. That is, taking norms as distances, the distance from point A through B to C is never shorter than going directly from A to C, or the shortest distance between any two points is a straight line.

In vector calculus and physics, a vector field is an assignment of a vector to each point in a subset of space. A vector field in the plane, can be visualised as: a collection of arrows with a given magnitude and direction, each attached to a point in the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout space, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.
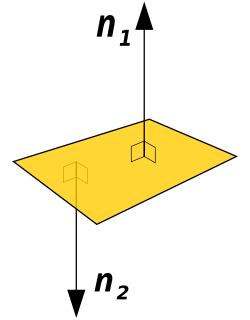
In geometry, a normal is an object such as a line or vector that is perpendicular to a given object. For example, in two dimensions, the normal line to a curve at a given point is the line perpendicular to the tangent line to the curve at the point.

In multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis.
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time evolution of a Hamiltonian dynamical system. The Poisson bracket also distinguishes a certain class of coordinate transformations, called canonical transformations, which map canonical coordinate systems into canonical coordinate systems. A "canonical coordinate system" consists of canonical position and momentum variables that satisfy canonical Poisson bracket relations. The set of possible canonical transformations is always very rich. For instance, it is often possible to choose the Hamiltonian itself as one of the new canonical momentum coordinates.
In differential geometry, the Lie derivative, named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a tensor field, along the flow defined by another vector field. This change is coordinate invariant and therefore the Lie derivative is defined on any differentiable manifold.
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is invertible, or equivalently that there are no real characteristic directions.

In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum to 1.
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.
In mathematics, specifically in the field of differential topology, Morse homology is a homology theory defined for any smooth manifold. It is constructed using the smooth structure and an auxiliary metric on the manifold, but turns out to be topologically invariant, and is in fact isomorphic to singular homology. Morse homology also serves as a model for the various infinite-dimensional generalizations known as Floer homology theories.
The envelope theorem is a result about the differentiability properties of the objective function of a parameterized optimization problem. As we change parameters of the objective, the envelope theorem shows that, in a certain sense, changes in the optimizer of the objective do not contribute to the change in the objective function. The envelope theorem is an important tool for comparative statics of optimization models.
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve.
In mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.

Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body.
A reference frame in which the time coordinate defines proper time for all co-moving observers is called "synchronous". It is built by choosing some time-like hypersurface as an origin, such that has in every point a normal along the time line ; all interval elements on this hypersurface are space-like. A family of geodesics normal to this hypersurface are drawn and defined as the time coordinates with a beginning at the hypersurface.
In continuum mechanics, a compatible deformation tensor field in a body is that unique tensor field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed. Compatibility conditions are particular cases of integrability conditions and were first derived for linear elasticity by Barré de Saint-Venant in 1864 and proved rigorously by Beltrami in 1886.
In mathematics, a free boundary problem is a partial differential equation to be solved for both an unknown function u and an unknown domain Ω. The segment Γ of the boundary of Ω which is not known at the outset of the problem is the free boundary.
In symplectic geometry, the spectral invariants are invariants defined for the group of Hamiltonian diffeomorphisms of a symplectic manifold, which is closed related to Floer theory and Hofer geometry.










