 | This article relies largely or entirely on a single source .(May 2024) |
In mathematics, a horn angle, also called a cornicular angle, is a type of curvilinear angle defined as the angle formed between a circle and a straight line tangent to it, or, more generally, the angle formed between two curves at a point where they are tangent to each other.
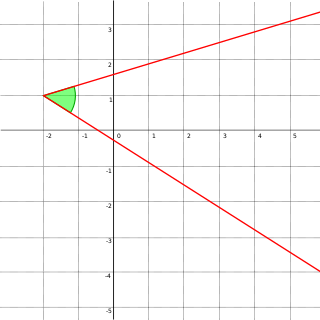
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays are also known as plane angles as they lie in the plane that contains the rays. Angles are also formed by the intersection of two planes; these are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. The distance between any point of the circle and the centre is called the radius.
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.
A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. Formally, a sphere is the set of points that are all at the same distance r from a given point in three-dimensional space. That given point is the center of the sphere, and r is the sphere's radius. The earliest known mentions of spheres appear in the work of the ancient Greek mathematicians.
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is tangent to the curve y = f(x) at a point x = c if the line passes through the point (c, f(c)) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
In geometry, a secant is a line that intersects a curve at a minimum of two distinct points. The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant intersects the circle at exactly two points. A chord is the line segment determined by the two points, that is, the interval on the secant whose ends are the two points.
The Elements is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid c. 300 BC. It is a collection of definitions, postulates, propositions, and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. Elements is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19th century.
In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. It is a circular arc that measures 180°. It has only one line of symmetry.
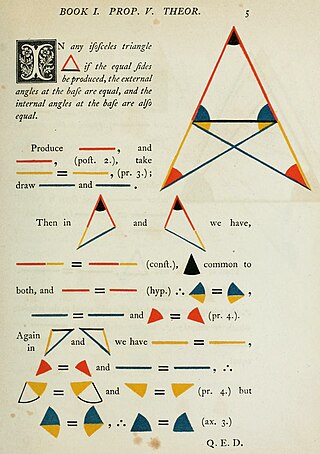
In geometry, the theorem that the angles opposite the equal sides of an isosceles triangle are themselves equal is known as the pons asinorum, Latin for "bridge of asses", or more descriptively as the isosceles triangle theorem. The theorem appears as Proposition 5 of Book 1 in Euclid's Elements. Its converse is also true: if two angles of a triangle are equal, then the sides opposite them are also equal.
In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.
The following outline is provided as an overview of and topical guide to trigonometry:
In geometry, a transversal is a line that passes through two lines in the same plane at two distinct points. Transversals play a role in establishing whether two or more other lines in the Euclidean plane are parallel. The intersections of a transversal with two lines create various types of pairs of angles: consecutive interior angles, consecutive exterior angles, corresponding angles, and alternate angles. As a consequence of Euclid's parallel postulate, if the two lines are parallel, consecutive interior angles are supplementary, corresponding angles are equal, and alternate angles are equal.
The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.
In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.
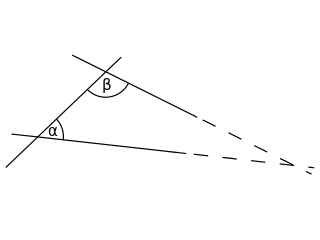
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.
In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid :
In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.
 | This elementary geometry-related article is a stub. You can help Wikipedia by expanding it. |