
In geometry, a regular icosahedron is a convex polyhedron with 20 faces, 30 edges and 12 vertices. It is one of the five Platonic solids, and the one with the most faces.
In combinatorial mathematics, a Steiner system is a type of block design, specifically a t-design with λ = 1 and t = 2 or (recently) t ≥ 2.
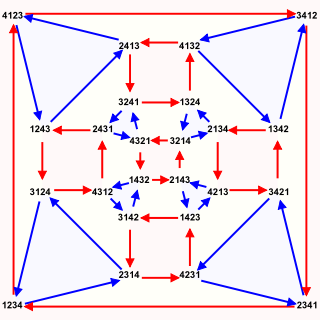
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group defined over a finite set of symbols consists of the permutations that can be performed on the symbols. Since there are such permutation operations, the order of the symmetric group is .

In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set.
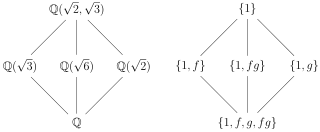
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to group theory, which makes them simpler and easier to understand.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.

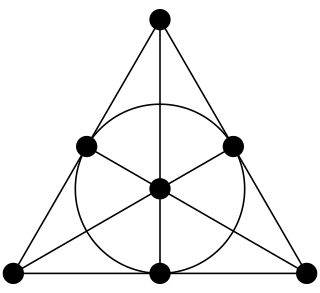
In finite geometry, the Fano plane is a finite projective plane with the smallest possible number of points and lines: 7 points and 7 lines, with 3 points on every line and 3 lines through every point. These points and lines cannot exist with this pattern of incidences in Euclidean geometry, but they can be given coordinates using the finite field with two elements. The standard notation for this plane, as a member of a family of projective spaces, is PG(2, 2). Here PG stands for "projective geometry", the first parameter is the geometric dimension and the second parameter is the order.

Pancake sorting is the mathematical problem of sorting a disordered stack of pancakes in order of size when a spatula can be inserted at any point in the stack and used to flip all pancakes above it. A pancake number is the minimum number of flips required for a given number of pancakes. In this form, the problem was first discussed by American geometer Jacob E. Goodman. A variant of the problem is concerned with burnt pancakes, where each pancake has a burnt side and all pancakes must, in addition, end up with the burnt side on bottom.
In mathematics, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1. Typically, mathematicians are interested in q-analogs that arise naturally, rather than in arbitrarily contriving q-analogs of known results. The earliest q-analog studied in detail is the basic hypergeometric series, which was introduced in the 19th century.
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence, construction and properties of systems of finite sets whose arrangements satisfy generalized concepts of balance and/or symmetry. These concepts are not made precise so that a wide range of objects can be thought of as being under the same umbrella. At times this might involve the numerical sizes of set intersections as in block designs, while at other times it could involve the spatial arrangement of entries in an array as in sudoku grids.

In the mathematical field of graph theory, the Hoffman–Singleton graph is a 7-regular undirected graph with 50 vertices and 175 edges. It is the unique strongly regular graph with parameters (50,7,0,1). It was constructed by Alan Hoffman and Robert Singleton while trying to classify all Moore graphs, and is the highest-order Moore graph known to exist. Since it is a Moore graph where each vertex has degree 7, and the girth is 5, it is a (7,5)-cage.

Thomas Penyngton Kirkman FRS was a British mathematician and ordained minister of the Church of England. Despite being primarily a churchman, he maintained an active interest in research-level mathematics, and was listed by Alexander Macfarlane as one of ten leading 19th-century British mathematicians. In the 1840s, he obtained an existence theorem for Steiner triple systems that founded the field of combinatorial design theory, while the related Kirkman's schoolgirl problem is named after him.

Galois geometry is the branch of finite geometry that is concerned with algebraic and analytic geometry over a finite field. More narrowly, a Galois geometry may be defined as a projective space over a finite field.

The 100 prisoners problem is a mathematical problem in probability theory and combinatorics. In this problem, 100 numbered prisoners must find their own numbers in one of 100 drawers in order to survive. The rules state that each prisoner may open only 50 drawers and cannot communicate with other prisoners. At first glance, the situation appears hopeless, but a clever strategy offers the prisoners a realistic chance of survival.
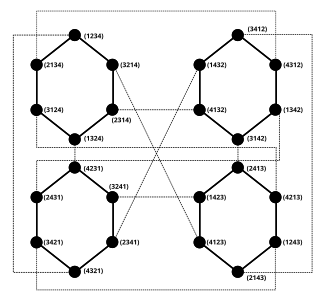
In the mathematical field of graph theory, the pancake graphPn or n-pancake graph is a graph whose vertices are the permutations of n symbols from 1 to n and its edges are given between permutations transitive by prefix reversals.
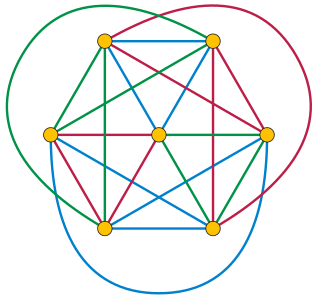
The Oberwolfach problem is an unsolved problem in mathematics that may be formulated either as a problem of scheduling seating assignments for diners, or more abstractly as a problem in graph theory, on the edge cycle covers of complete graphs. It is named after the Oberwolfach Research Institute for Mathematics, where the problem was posed in 1967 by Gerhard Ringel. It is known to be true for all sufficiently-large complete graphs.
Lu Jiaxi was a self-taught Chinese mathematician who made important contributions in combinatorial design theory. He was a high school physics teacher in a remote city and worked in his spare time on the problem of large sets of disjoint Steiner triple systems.

In finite geometry, PG(3,2) is the smallest three-dimensional projective space. It can be thought of as an extension of the Fano plane. It has 15 points, 35 lines, and 15 planes. It also has the following properties:

In combinatorics, tripod packing is a problem of finding many disjoint tripods in a three-dimensional grid, where a tripod is an infinite polycube, the union of the grid cubes along three positive axis-aligned rays with a shared apex.
In discrete mathematics, the social golfer problem (SGP) is a combinatorial-design problem derived from a question posted in the usenet newsgroup sci.op-research in May 1998. The problem is as follows: 32 golfers play golf once a week in groups of 4. Schedule these golfers to play for as many weeks as possible without any two golfers playing together in a group more than once.




























