
The steradian or square radian is the unit of solid angle in the International System of Units (SI). It is used in three dimensional geometry, and is analogous to the radian, which quantifies planar angles. Whereas an angle in radians, projected onto a circle, gives a length of a circular arc on the circumference, a solid angle in steradians, projected onto a sphere, gives the area of a spherical cap on the surface. The name is derived from the Greek στερεός stereos 'solid' + radian.

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.
In geometry, a solid angle is a measure of the amount of the field of view from some particular point that a given object covers. That is, it is a measure of how large the object appears to an observer looking from that point. The point from which the object is viewed is called the apex of the solid angle, and the object is said to subtend its solid angle at that point.

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

The great-circle distance, orthodromic distance, or spherical distance is the distance along a great circle.

Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are great circles. Spherical trigonometry is of great importance for calculations in astronomy, geodesy, and navigation.

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron and of a Johnson solid.

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.

In spherical trigonometry, the law of cosines is a theorem relating the sides and angles of spherical triangles, analogous to the ordinary law of cosines from plane trigonometry.
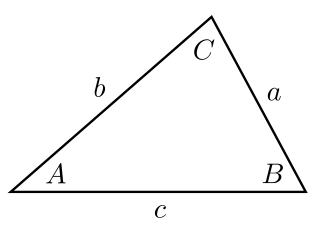
In mathematics, Weitzenböck's inequality, named after Roland Weitzenböck, states that for a triangle of side lengths , , , and area , the following inequality holds:

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:

In geometry, an equilateral pentagon is a polygon in the Euclidean plane with five sides of equal length. Its five vertex angles can take a range of sets of values, thus permitting it to form a family of pentagons. In contrast, the regular pentagon is unique, because it is equilateral and moreover it is equiangular.

Geographical distance or geodetic distance is the distance measured along the surface of the Earth, or the shortest arch length.

In trigonometry, Mollweide's formula is a pair of relationships between sides and angles in a triangle.
Solution of triangles is the main trigonometric problem of finding the characteristics of a triangle, when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation.
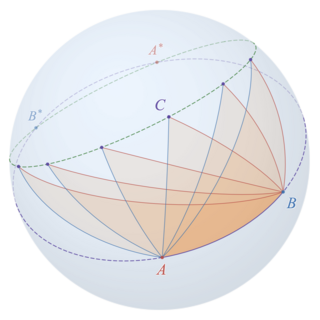
In spherical geometry, Lexell's theorem holds that every spherical triangle with the same surface area on a fixed base has its apex on a small circle, called Lexell's circle or Lexell's locus, passing through each of the two points antipodal to the two base vertices.


















