In mathematics, the prime number theorem (PNT) describes the asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by precisely quantifying the rate at which this occurs. The theorem was proved independently by Jacques Hadamard and Charles Jean de la Vallée Poussin in 1896 using ideas introduced by Bernhard Riemann.

The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter ζ (zeta), is a mathematical function of a complex variable defined as
The Liouville lambda function, denoted by λ(n) and named after Joseph Liouville, is an important arithmetic function. Its value is +1 if n is the product of an even number of prime numbers, and −1 if it is the product of an odd number of primes.
In the calculus of variations, a field of mathematical analysis, the functional derivative relates a change in a functional to a change in a function on which the functional depends.
In mathematical physics, n-dimensional de Sitter space is a maximally symmetric Lorentzian manifold with constant positive scalar curvature. It is the Lorentzian analogue of an n-sphere.

In mathematics, the prime-counting function is the function counting the number of prime numbers less than or equal to some real number x. It is denoted by π(x) (unrelated to the number π).

In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum.
In mathematics, the ratio test is a test for the convergence of a series

In number theory, the Mertens function is defined for all positive integers n as

In mathematics, the polylogarithm (also known as Jonquière's function, for Alfred Jonquière) is a special function Lis(z) of order s and argument z. Only for special values of s does the polylogarithm reduce to an elementary function such as the natural logarithm or a rational function. In quantum statistics, the polylogarithm function appears as the closed form of integrals of the Fermi–Dirac distribution and the Bose–Einstein distribution, and is also known as the Fermi–Dirac integral or the Bose–Einstein integral. In quantum electrodynamics, polylogarithms of positive integer order arise in the calculation of processes represented by higher-order Feynman diagrams.
In the theory of stochastic processes, the Karhunen–Loève theorem, also known as the Kosambi–Karhunen–Loève theorem states that a stochastic process can be represented as an infinite linear combination of orthogonal functions, analogous to a Fourier series representation of a function on a bounded interval. The transformation is also known as Hotelling transform and eigenvector transform, and is closely related to principal component analysis (PCA) technique widely used in image processing and in data analysis in many fields.
In mathematics, the Lerch zeta function, sometimes called the Hurwitz–Lerch zeta function, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after Czech mathematician Mathias Lerch, who published a paper about the function in 1887.

In mathematics, the Riesz function is an entire function defined by Marcel Riesz in connection with the Riemann hypothesis, by means of the power series
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt. It is an example of an important arithmetic function that is neither multiplicative nor additive.
In mathematics, the explicit formulae for L-functions are relations between sums over the complex number zeroes of an L-function and sums over prime powers, introduced by Riemann (1859) for the Riemann zeta function. Such explicit formulae have been applied also to questions on bounding the discriminant of an algebraic number field, and the conductor of a number field.

In mathematics (specifically multivariable calculus), a multiple integral is a definite integral of a function of several real variables, for instance, f(x, y) or f(x, y, z). Integrals of a function of two variables over a region in (the real-number plane) are called double integrals, and integrals of a function of three variables over a region in (real-number 3D space) are called triple integrals. For multiple integrals of a single-variable function, see the Cauchy formula for repeated integration.
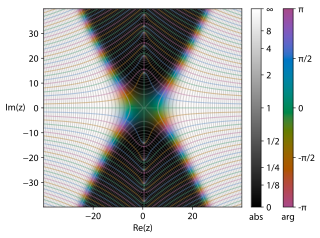
In mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation. The function is named in honour of Bernhard Riemann.

In mathematics, the Chebyshev function is either a scalarising function (Tchebycheff function) or one of two related functions. The first Chebyshev functionϑ (x) or θ (x) is given by

In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part 1/2. Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by Bernhard Riemann (1859), after whom it is named.
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.















































