Limiting parallel

Last updated August 11, 2019

In neutral or absolute geometry, and in hyperbolic geometry, there may be many lines parallel to a given line $l$ through a point $P$ not on line $R$ ; however, in the plane, two parallels may be closer to $l$ than all others (one in each direction of $R$ ).

Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not sufficient as a basis of Euclidean geometry, other systems, such as Hilbert's axioms without the parallel axiom, are used. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate.

Hyperbolic geometry Non-Euclidean geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

Greek is an independent branch of the Indo-European family of languages, native to Greece, Cyprus and other parts of the Eastern Mediterranean and the Black Sea. It has the longest documented history of any living Indo-European language, spanning more than 3000 years of written records. Its writing system has been the Greek alphabet for the major part of its history; other systems, such as Linear B and the Cypriot syllabary, were used previously. The alphabet arose from the Phoenician script and was in turn the basis of the Latin, Cyrillic, Armenian, Coptic, Gothic, and many other writing systems.

For rays, the relation of limiting parallel is an equivalence relation, which includes the equivalence relation of being coterminal.

In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The relation "is equal to" is the canonical example of an equivalence relation, where for any objects $a$ , $b$ , and $c$ :

If, in a hyperbolic triangle, the pairs of sides are limiting parallel, then the triangle is an ideal triangle.

In hyperbolic geometry, a hyperbolic triangle is a triangle in the hyperbolic plane. It consists of three line segments called sides or edges and three points called angles or vertices.

In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all are ideal points. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles. The vertices are sometimes called ideal vertices. All ideal triangles are congruent.

Definition

A ray $Aa$ is a limiting parallel to a ray $Bb$ if they are coterminal or if they lie on distinct lines not equal to the line $AB$ , they do not meet, and every ray in the interior of the angle $BAa$ meets the ray $Bb$ .^[1]

Properties

Distinct lines carrying limiting parallel rays do not meet.

Proof

Suppose that the lines carrying distinct parallel rays met. By definition they cannot meet on the side of $AB$ which either $a$ is on. Then they must meet on the side of $AB$ opposite to $a$ , call this point $C$ . Thus $\angle CAB+\angle CBA<2{\text{ right angles}}\Rightarrow \angle aAB+\angle bBA>2{\text{ right angles}}$ . Contradiction.

Related Research Articles

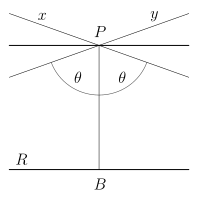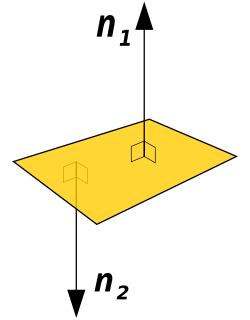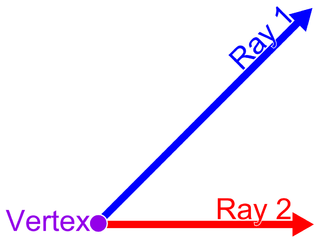
In plane geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in a plane, but this plane does not have to be a Euclidean plane. Angles are also formed by the intersection of two planes in Euclidean and other spaces. These are called dihedral angles. Angles formed by the intersection of two curves in a plane are defined as the angle determined by the tangent rays at the point of intersection. Similar statements hold in space, for example, the spherical angle formed by two great circles on a sphere is the dihedral angle between the planes determined by the great circles.

Right triangle triangle in which one angle is a 90-degree angle

A right triangle or right-angled triangle is a triangle in which one angle is a right angle. The relation between the sides and angles of a right triangle is the basis for trigonometry.

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal. It can also be defined as a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term oblong is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.

Perpendicular Relationship between two lines that meet at a right angle (90 degrees)

In elementary geometry, the property of being perpendicular (perpendicularity) is the relationship between two lines which meet at a right angle. The property extends to other related geometric objects.

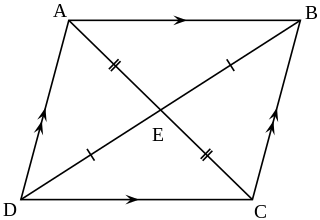
Parallelogram quadrilateral with two pairs of parallel sides

In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.

In mathematics, affine geometry is what remains of Euclidean geometry when not using the metric notions of distance and angle.

In geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, or. It can also be defined as a rectangle in which two adjacent sides have equal length. A square with vertices ABCD would be denoted $ABCD .$

In geometry, parallel lines are lines in a plane which do not meet; that is, two lines in a plane that do not intersect or touch each other at any point are said to be parallel. By extension, a line and a plane, or two planes, in three-dimensional Euclidean space that do not share a point are said to be parallel. However, two lines in three-dimensional space which do not meet must be in a common plane to be considered parallel; otherwise they are called skew lines. Parallel planes are planes in the same three-dimensional space that never meet.

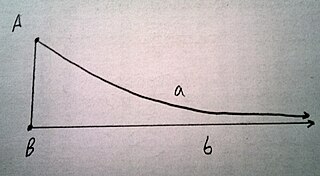
In hyperbolic geometry, the angle of parallelism $, is the angle at one vertex of a right hyperbolic triangle that has two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.$

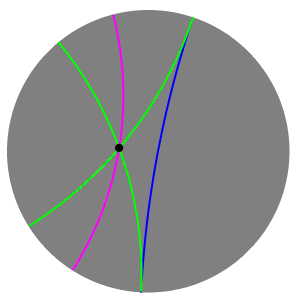
In hyperbolic geometry, two lines may intersect, be ultraparallel, or be limiting parallel.

In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle. Each triangle group is the symmetry group of a tiling of the Euclidean plane, the sphere, or the hyperbolic plane by congruent triangles called Möbius triangles, each one a fundamental domain for the action.

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of hyperbolic geometry in which points are represented by the points in the interior of the unit disk and lines are represented by the chords, straight line segments with ideal endpoints on the boundary sphere.

In hyperbolic geometry, an ideal point, omega point or point at infinity is a well defined point outside the hyperbolic plane or space. Given a line l and a point P not on l, right- and left-limiting parallels to l through P converge to l at ideal points.

Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement. Ordered geometry is a fundamental geometry forming a common framework for affine, Euclidean, absolute, and hyperbolic geometry.

Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

Playfairs axiom Modern formulation of Euclids parallel postulate

In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid :

In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.

Hyperbolic geometry is a non-Euclidean geometry where the first four axioms of Euclidean geometry are kept but the fifth axiom, the parallel postulate, is changed. The fifth axiom of hyperbolic geometry says that given a line L and a point P not on that line, there are at least two lines passing through P that are parallel to L. As in Euclidean geometry, where ancient Greek mathematicians used a compass and idealized ruler for constructions of lengths, angles, and other geometric figures, constructions can also be made in hyperbolic geometry.

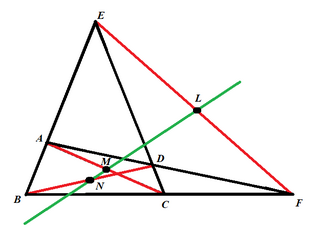
In geometry, the Newton–Gauss line is the line joining the midpoints of the three diagonals of a complete quadrilateral.

References

↑ Hartshorne, Robin (2000). Geometry: Euclid and beyond (Corr. 2nd print. ed.). New York, NY [u.a.]: Springer. ISBN 978-0-387-98650-0.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Hartshorne, Robin (2000). Geometry: Euclid and beyond (Corr. 2nd print. ed.). New York, NY [u.a.]: Springer. ISBN 978-0-387-98650-0.