 | This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations .(August 2022) |
In metaphysics, the multiple occupancy view (m.o.) is a particular analysis of fission cases[ clarification needed ], which claims to be at least a priori possible, if not actually true of real cases of fission.
Imagine an amoeba which undergoes symmetrical fission into two sister amoebae (call them B and C). We tend to think that before fission there was one amoeba (call it A), but what has happened to it? It has not died, for death is a biological state, and there are no dead amoebae lying around after the fission! In fact, there is more life after the fission than there was before, i.e. two live amoebae instead of just one. Has A somehow ceased to exist without dying? Is A still around, and identical with either B or C? It cannot be identified with both B and C, for identity is a transitive relation, and B is certainly not the same amoeba as C. Yet, the fission was symmetrical, so neither B nor C has any more or less claim to be A than the other.
This is the problem. We seem to be forced to say that A has ceased to exist, but the m.o. view provides us with another option, consistent with all of the above considerations. The m.o. view is that there were two distinct but coincident amoebae before fission, occupying the same body of matter, but which diverge upon fission into the same two distinct, but no longer coincident, amoebae. The number of amoebae hasn't increased, i.e. there were two before fission, and there are the same two after fission. The amoeba has "divided without multiplying"!
The m.o. view has also been applied to hypothetical cases of symmetrical fission involving persons. On the face of it, the m.o. view contravenes the principle of identity of indiscernibles. However, one and the same physical object can be a proper part of two or more distinct objects (e.g., a road intersection is part of two distinct roads), which leads to four-dimensionalism, whereby, for example, an amoeba at a time (amoeba stage) is a temporal part of an amoeba extended in time, i.e., objects have temporal parts.
Entamoeba is a genus of Amoebozoa found as internal parasites or commensals of animals.
In abstract algebra, a branch of mathematics, a monoid is a set equipped with an associative binary operation and an identity element. For example, the nonnegative integers with addition form a monoid, the identity element being 0.
Slime mold or slime mould is an informal name given to several kinds of unrelated eukaryotic organisms with a life cycle that includes a free-living single-celled stage and the formation of spores. Spores are often produced in macroscopic multicellular or multinucleate fruiting bodies which may be formed through aggregation or fusion. Slime molds were formerly classified as fungi but are no longer considered part of that kingdom. Although not forming a single monophyletic clade, they are grouped within the paraphyletic group Protista.
In mathematics, a category is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions.
In philosophy, identity is the relation each thing bears only to itself. The notion of identity gives rise to many philosophical problems, including the identity of indiscernibles, and questions about change and personal identity over time. It is important to distinguish between qualitative identity and numerical identity. For example, consider two children with identical bicycles engaged in a race while their mother is watching. The two children have the same bicycle in one sense and the same mother in another sense. This article is mainly concerned with numerical identity, which is the stricter notion.
In mathematics, equality is a relationship between two quantities or, more generally two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object. The equality between A and B is written A = B, and pronounced A equals B. The symbol "=" is called an "equals sign". Two objects that are not equal are said to be distinct.
In category theory, a branch of mathematics, an enriched category generalizes the idea of a category by replacing hom-sets with objects from a general monoidal category. It is motivated by the observation that, in many practical applications, the hom-set often has additional structure that should be respected, e.g., that of being a vector space of morphisms, or a topological space of morphisms. In an enriched category, the set of morphisms associated with every pair of objects is replaced by an object in some fixed monoidal category of "hom-objects". In order to emulate the (associative) composition of morphisms in an ordinary category, the hom-category must have a means of composing hom-objects in an associative manner: that is, there must be a binary operation on objects giving us at least the structure of a monoidal category, though in some contexts the operation may also need to be commutative and perhaps also to have a right adjoint.
In mathematics, a monoidal category is a category equipped with a bifunctor
Philosophy of space and time is the branch of philosophy concerned with the issues surrounding the ontology and epistemology of space and time. While such ideas have been central to philosophy from its inception, the philosophy of space and time was both an inspiration for and a central aspect of early analytic philosophy. The subject focuses on a number of basic issues, including whether time and space exist independently of the mind, whether they exist independently of one another, what accounts for time's apparently unidirectional flow, whether times other than the present moment exist, and questions about the nature of identity.
Named after the 19th century British mathematician Arthur Cayley, a Cayley table describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table. Many properties of a group – such as whether or not it is abelian, which elements are inverses of which elements, and the size and contents of the group's center – can be discovered from its Cayley table.
Perdurantism or perdurance theory is a philosophical theory of persistence and identity. The debate over persistence currently involves three competing theories—one three-dimensionalist theory called "endurantism" and two four-dimensionalist theories called "perdurantism" and "exdurantism". For a perdurantist, all objects are considered to be four-dimensional worms and they make up the different regions of spacetime. It is a fusion of all the perdurant's instantaneous time slices compiled and blended into a complete mereological whole. Perdurantism posits that temporal parts alone are what ultimately change. David Lewis in "On The Plurality of World" states that change is "the possession of different properties by different temporal parts of an object" (12).
In philosophy, four-dimensionalism is the ontological position that an object's persistence through time is like its extension through space. Thus, an object that exists in time has temporal parts in the various subregions of the total region of time it occupies, just like an object that exists in a region of space has at least one part in every subregion of that space.
The B-theory of time, also called the "tenseless theory of time", is one of two positions regarding the temporal ordering of events in the philosophy of time. B-theorists argue that the flow of time is only a subjective illusion of human consciousness, that the past, present, and future are equally real, and that time is tenseless: temporal becoming is not an objective feature of reality. Therefore, there is nothing privileged about the present, ontologically speaking.
In philosophy, specifically in the area of metaphysics, counterpart theory is an alternative to standard (Kripkean) possible-worlds semantics for interpreting quantified modal logic. Counterpart theory still presupposes possible worlds, but differs in certain important respects from the Kripkean view. The form of the theory most commonly cited was developed by David Lewis, first in a paper and later in his book On the Plurality of Worlds.
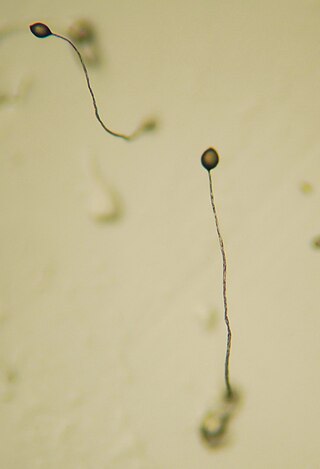
Dictyostelium discoideum is a species of soil-dwelling amoeba belonging to the phylum Amoebozoa, infraphylum Mycetozoa. Commonly referred to as slime mold, D. discoideum is a eukaryote that transitions from a collection of unicellular amoebae into a multicellular slug and then into a fruiting body within its lifetime. Its unique asexual lifecycle consists of four stages: vegetative, aggregation, migration, and culmination. The lifecycle of D. discoideum is relatively short, which allows for timely viewing of all stages. The cells involved in the lifecycle undergo movement, chemical signaling, and development, which are applicable to human cancer research. The simplicity of its lifecycle makes D. discoideum a valuable model organism to study genetic, cellular, and biochemical processes in other organisms.
Sappinia is a genus of heterotrophic, lobose amoebae within the family Thecamoebidae. A defining feature of Sappinia, which separates it from its sister genus Thecamoeba, is the presence of two closely apposed nuclei with a central, flattened connection. Sappinia species have two life cycle stages: a trophozoite and a cyst. Up until 2015, only two species had been discovered, Sappinia pedata and Sappinia diploidea. Sequencing of the small subunit rRNA of a particular isolate from a sycamore tree revealed a new species, Sappinia platani.Sappinia species were once thought to be coprozoic, as the first strains were isolated from animal dung. More research has shown that they are typical free-living amoebae, and can be found worldwide in soil, plant litter, and standing decaying plants, as well as freshwater ponds. In 2001, the first and only case of human pathogenesis in Sappinia was confirmed. The patient was a non-immunocompromised 38-year-old male who presented signs of amoebic encephalitis and who patient made a full recovery after treatment with several antimicrobials. The CDC initially classified the causative agent as S. diploidea based on morphological characteristics, but in 2009, Qvarnstrom et al. used molecular data to confirm that the true causative agent was S. pedata.
Testate amoebae are a polyphyletic group of unicellular amoeboid protists, which differ from naked amoebae in the presence of a test that partially encloses the cell, with an aperture from which the pseudopodia emerge, that provides the amoeba with shelter from predators and environmental conditions.
Parachlamydia acanthamoebae are bacterium that fall into the category of host-associated microorganisms. This bacterium lives within free-living amoebae that are an intricate part of their reproduction. Originally named Candidatus Parachlamydia acanthamoebae, its current scientific name was introduced shortly after. This species has shown to have over eighty percent 16S rRNA gene sequencing identity with the class Chlamydiia. Parachlamydia acanthamoebae has the same family as the genus Neochlamydia with which it shares many similarities.
An amoeba, often called an amoeboid, is a type of cell or unicellular organism with the ability to alter its shape, primarily by extending and retracting pseudopods. Amoebae do not form a single taxonomic group; instead, they are found in every major lineage of eukaryotic organisms. Amoeboid cells occur not only among the protozoa, but also in fungi, algae, and animals.
Naegleria fowleri, colloquially known as a "brain-eating amoeba", is a species of the genus Naegleria, belonging to the phylum Percolozoa, which is technically not classified as true amoeba, but a shapeshifting amoeboflagellate excavate. It is a free-living, bacteria-eating microorganism that can be pathogenic, causing an extremely rare, sudden, severe and usually fatal brain infection called naegleriasis or primary amoebic meningoencephalitis (PAM). This microorganism is typically found in bodies of warm freshwater, such as ponds, lakes, rivers, hot springs, warm water discharge from industrial or power plants, geothermal well water, poorly maintained or minimally chlorinated swimming pools, water heaters, soil, and pipes connected to tap water. It can be seen in either an amoeboid or temporary flagellate stage.
 | This article about metaphysics is a stub. You can help Wikipedia by expanding it. |