Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.
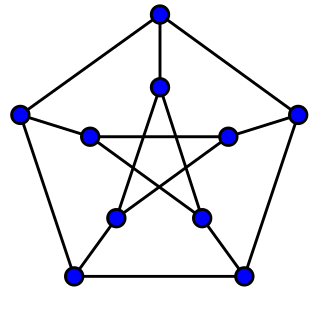
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.
Graph pebbling is a mathematical game played on a graph with zero or more pebbles on each of its vertices. 'Game play' is composed of a series of pebbling moves. A pebbling move on a graph consists of choosing a vertex with at least two pebbles, removing two pebbles from it, and adding one to an adjacent vertex (the second removed pebble is discarded from play). π(G), the pebbling number of a graph G, is the lowest natural number n that satisfies the following condition:
Given any target or 'root' vertex in the graph and any initial configuration of n pebbles on the graph, it is possible, after a series of pebbling moves, to reach a new configuration in which the designated root vertex has one or more pebbles.

In combinatorics, a k-ary necklace of length n is an equivalence class of n-character strings over an alphabet of size k, taking all rotations as equivalent. It represents a structure with n circularly connected beads which have k available colors.

Discrete tomography focuses on the problem of reconstruction of binary images from a small number of their projections.

In graph theory, a branch of mathematics, the handshaking lemma is the statement that, in every finite undirected graph, the number of vertices that touch an odd number of edges is even. For example, if there is a party of people who shake hands, the number of people who shake an odd number of other people's hands is even. The handshaking lemma is a consequence of the degree sum formula, also sometimes called the handshaking lemma, according to which the sum of the degrees equals twice the number of edges in the graph. Both results were proven by Leonhard Euler (1736) in his famous paper on the Seven Bridges of Königsberg that began the study of graph theory.
The mathematical discipline of topological combinatorics is the application of topological and algebro-topological methods to solving problems in combinatorics.
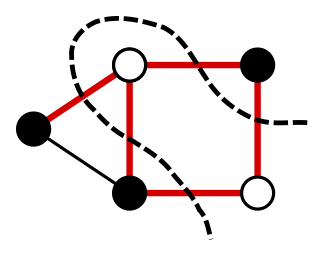
For a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets S and T, such that the number of edges between S and T is as large as possible. Finding such a cut is known as the max-cut problem.
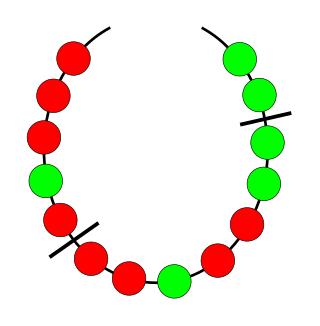
Necklace splitting is a picturesque name given to several related problems in combinatorics and measure theory. Its name and solutions are due to mathematicians Noga Alon and Douglas B. West.
In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices {u1, u2, …, un} and {v1, v2, …, vn} and with an edge from ui to vj whenever i ≠ j.
In computer science and graph theory, the term color-coding refers to an algorithmic technique which is useful in the discovery of network motifs. For example, it can be used to detect a simple path of length k in a given graph. The traditional color-coding algorithm is probabilistic, but it can be derandomized without much overhead in the running time.
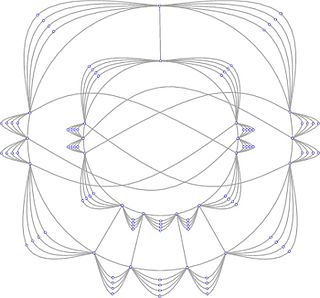
In mathematics, a topological graph is a representation of a graph in the plane, where the vertices of the graph are represented by distinct points and the edges by Jordan arcs joining the corresponding pairs of points. The points representing the vertices of a graph and the arcs representing its edges are called the vertices and the edges of the topological graph. It is usually assumed that any two edges of a topological graph cross a finite number of times, no edge passes through a vertex different from its endpoints, and no two edges touch each other. A topological graph is also called a drawing of a graph.

Italo Jose Dejter is an Argentine-born American mathematician, a retired professor of mathematics and computer science from the University of Puerto Rico, and a researcher in algebraic topology, differential topology, graph theory, coding theory and combinatorial designs. He obtained a Licentiate degree in mathematics from University of Buenos Aires in 1967, arrived at Rutgers University in 1970 by means of a Guggenheim Fellowship and obtained a Ph.D. degree in mathematics in 1975 under the supervision of Professor Ted Petrie, with support of the National Science Foundation. He was a professor at the Federal University of Santa Catarina, Brazil, from 1977 to 1984, with grants from the National Council for Scientific and Technological Development, (CNPq).
In combinatorial mathematics, probability, and computer science, in the longest alternating subsequence problem, one wants to find a subsequence of a given sequence in which the elements are in alternating order, and in which the sequence is as long as possible.
In the mathematical field of graph theory, the Dejter graph is a 6-regular graph with 112 vertices and 336 edges. The Dejter graph is obtained by deleting a copy of the Hamming code of length 7 from the binary 7-cube.
Wojciech Samotij is a Polish mathematician and an associate professor at the School of Mathematical Sciences at the Tel Aviv University. He is known for his work in combinatorics, additive number theory, Ramsey theory and graph theory.

In computational complexity theory, a planted clique or hidden clique in an undirected graph is a clique formed from another graph by selecting a subset of vertices and adding edges between each pair of vertices in the subset. The planted clique problem is the algorithmic problem of distinguishing random graphs from graphs that have a planted clique. This is a variation of the clique problem; it may be solved in quasi-polynomial time but is conjectured not to be solvable in polynomial time for intermediate values of the clique size. The conjecture that no polynomial time solution exists is called the planted clique conjecture; it has been used as a computational hardness assumption.
In the mathematical field of graph theory, a word-representable graph is a graph that can be characterized by a word whose entries alternate in a prescribed way. In particular, if the vertex set of the graph is V, one should be able to choose a word w over the alphabet V such that letters a and b alternate in w if and only if the pair ab is an edge in the graph. For example, the cycle graph labeled by a, b, c and d in clock-wise direction is word-representable because it can be represented by abdacdbc: the pairs ab, bc, cd and ad alternate, but the pairs ac and bd do not.

In graph theory, the Graham–Pollak theorem states that the edges of an -vertex complete graph cannot be partitioned into fewer than complete bipartite graphs. It was first published by Ronald Graham and Henry O. Pollak in two papers in 1971 and 1972, in connection with an application to telephone switching circuitry.


















