
In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency. One needs a definition of intersection number in order to state results like Bézout's theorem.
In mathematics, the Poincaré lemma gives a sufficient condition for a closed differential form to be exact. Precisely, it states that every closed p-form on an open ball in Rn is exact for p with 1 ≤ p ≤ n. The lemma was introduced by Henri Poincaré in 1886.
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For two bodies interacting by Newtonian gravity, the LRL vector is a constant of motion, meaning that it is the same no matter where it is calculated on the orbit; equivalently, the LRL vector is said to be conserved. More generally, the LRL vector is conserved in all problems in which two bodies interact by a central force that varies as the inverse square of the distance between them; such problems are called Kepler problems.
In functional analysis, the Friedrichs extension is a canonical self-adjoint extension of a non-negative densely defined symmetric operator. It is named after the mathematician Kurt Friedrichs. This extension is particularly useful in situations where an operator may fail to be essentially self-adjoint or whose essential self-adjointness is difficult to show.
In computer science, in particular in formal language theory, the pumping lemma for context-free languages, also known as the Bar-Hillel lemma, is a lemma that gives a property shared by all context-free languages and generalizes the pumping lemma for regular languages.
In convex analysis and the calculus of variations, both branches of mathematics, a pseudoconvex function is a function that behaves like a convex function with respect to finding its local minima, but need not actually be convex. Informally, a differentiable function is pseudoconvex if it is increasing in any direction where it has a positive directional derivative. The property must hold in all of the function domain, and not only for nearby points.

In mathematics, the classical groups are defined as the special linear groups over the reals , the complex numbers and the quaternions together with special automorphism groups of symmetric or skew-symmetric bilinear forms and Hermitian or skew-Hermitian sesquilinear forms defined on real, complex and quaternionic finite-dimensional vector spaces. Of these, the complex classical Lie groups are four infinite families of Lie groups that together with the exceptional groups exhaust the classification of simple Lie groups. The compact classical groups are compact real forms of the complex classical groups. The finite analogues of the classical groups are the classical groups of Lie type. The term "classical group" was coined by Hermann Weyl, it being the title of his 1939 monograph The Classical Groups.
In mathematics and mathematical physics, raising and lowering indices are operations on tensors which change their type. Raising and lowering indices are a form of index manipulation in tensor expressions.

Peridynamics is a non-local formulation of continuum mechanics that is oriented toward deformations with discontinuities, especially fractures. Originally, bond-based peridynamic has been introduced, wherein, internal interaction forces between a material point and all the other ones with which it can interact, are modeled as a central forces field. This type of force fields can be imagined as a mesh of bonds connecting each point of the body with every other interacting point within a certain distance which depends on material property, called peridynamic horizon. Later, to overcome bond-based framework limitations for the material Poisson’s ratio, state-base peridynamics, has been formulated. Its characteristic feature is that the force exchanged between a point and another one is influenced by the deformation state of all other bonds relative to its interaction zone.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation, Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.
In fracture mechanics, the energy release rate, , is the rate at which energy is transformed as a material undergoes fracture. Mathematically, the energy release rate is expressed as the decrease in total potential energy per increase in fracture surface area, and is thus expressed in terms of energy per unit area. Various energy balances can be constructed relating the energy released during fracture to the energy of the resulting new surface, as well as other dissipative processes such as plasticity and heat generation. The energy release rate is central to the field of fracture mechanics when solving problems and estimating material properties related to fracture and fatigue.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are called cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
The uncertainty theory invented by Baoding Liu is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms.
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
Parikh's theorem in theoretical computer science says that if one looks only at the number of occurrences of each terminal symbol in a context-free language, without regard to their order, then the language is indistinguishable from a regular language. It is useful for deciding that strings with a given number of terminals are not accepted by a context-free grammar. It was first proved by Rohit Parikh in 1961 and republished in 1966.
The invariant extended Kalman filter (IEKF) (not to be confused with the iterated extended Kalman filter) was first introduced as a version of the extended Kalman filter (EKF) for nonlinear systems possessing symmetries (or invariances), then generalized and recast as an adaptation to Lie groups of the linear Kalman filtering theory. Instead of using a linear correction term based on a linear output error, the IEKF uses a geometrically adapted correction term based on an invariant output error; in the same way the gain matrix is not updated from a linear state error, but from an invariant state error. The main benefit is that the gain and covariance equations have reduced dependence on the estimated value of the state. In some cases they converge to constant values on a much bigger set of trajectories than is the case for the EKF, which results in a better convergence of the estimation.
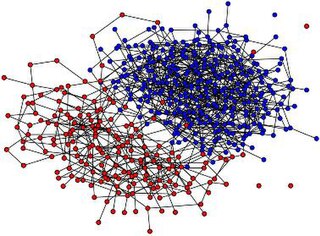
In the mathematical theory of probability, the voter model is an interacting particle system introduced by Richard A. Holley and Thomas M. Liggett in 1975.
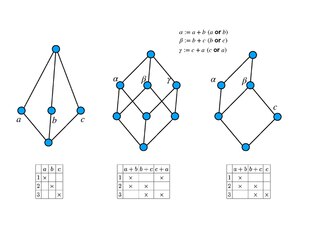
The General Concept Lattice (GCL) proposes a novel general construction of concept hierarchy from formal context, where the conventional Formal Concept Lattice based on Formal Concept Analysis (FCA) only serves as a substructure.
























































