Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry, Elements. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated earlier, Euclid was the first to organize these propositions into a logical system in which each result is proved from axioms and previously proved theorems.
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points to Euclidean points, and vice versa.

In mathematics, affine geometry is what remains of Euclidean geometry when ignoring the metric notions of distance and angle.

A finite geometry is any geometric system that has only a finite number of points. The familiar Euclidean geometry is not finite, because a Euclidean line contains infinitely many points. A geometry based on the graphics displayed on a computer screen, where the pixels are considered to be the points, would be a finite geometry. While there are many systems that could be called finite geometries, attention is mostly paid to the finite projective and affine spaces because of their regularity and simplicity. Other significant types of finite geometry are finite Möbius or inversive planes and Laguerre planes, which are examples of a general type called Benz planes, and their higher-dimensional analogs such as higher finite inversive geometries.
Synthetic geometry is geometry without the use of coordinates. It relies on the axiomatic method for proving all results from a few basic properties initially called postulate, and at present called axioms.
Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate. The first four of Euclid's postulates are now considered insufficient as a basis of Euclidean geometry, so other systems are used instead.
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie as the foundation for a modern treatment of Euclidean geometry. Other well-known modern axiomatizations of Euclidean geometry are those of Alfred Tarski and of George Birkhoff.

In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimension one, which may be embedded in spaces of dimension two, three, or higher. The word line may also refer, in everyday life, to a line segment, which is a part of a line delimited by two points.
In geometry, Pasch's theorem, stated in 1882 by the German mathematician Moritz Pasch, is a result in plane geometry which cannot be derived from Euclid's postulates.
In mathematics, Hilbert's fourth problem in the 1900 list of Hilbert's problems is a foundational question in geometry. In one statement derived from the original, it was to find — up to an isomorphism — all geometries that have an axiomatic system of the classical geometry, with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.
Tarski's axioms are an axiom system for Euclidean geometry, specifically for that portion of Euclidean geometry that is formulable in first-order logic with identity. As such, it does not require an underlying set theory. The only primitive objects of the system are "points" and the only primitive predicates are "betweenness" and "congruence". The system contains infinitely many axioms.

Moritz Pasch was a German mathematician of Jewish ancestry specializing in the foundations of geometry. He completed his Ph.D. at the University of Breslau at only 22 years of age. He taught at the University of Giessen, where he is known to have supervised 30 doctorates.
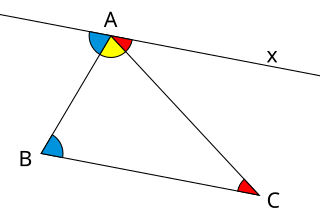
In a Euclidean space, the sum of angles of a triangle equals the straight angle . A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides.
Ordered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement. Ordered geometry is a fundamental geometry forming a common framework for affine, Euclidean, absolute, and hyperbolic geometry.
The exterior angle theorem is Proposition 1.16 in Euclid's Elements, which states that the measure of an exterior angle of a triangle is greater than either of the measures of the remote interior angles. This is a fundamental result in absolute geometry because its proof does not depend upon the parallel postulate.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.

In geometry, the crossbar theorem states that if ray AD is between ray AC and ray AB, then ray AD intersects line segment BC.

In geometry, Playfair's axiom is an axiom that can be used instead of the fifth postulate of Euclid :
In a plane, given a line and a point not on it, at most one line parallel to the given line can be drawn through the point.
In geometry, the point–line–plane postulate is a collection of assumptions (axioms) that can be used in a set of postulates for Euclidean geometry in two, three or more dimensions.